题目内容
设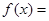
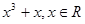，当0
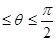时，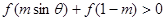
恒成立，则实数
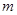的取值范围是 （ ）
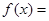
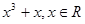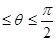，当0时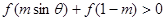，恒成立，则实数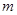的取值范围是 （ ）| A．（0,1） | B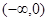． | C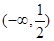． | D． |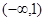
D
由f（x）=x3+x，可知f（x）为奇函数，增函数，得出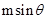
＞m-1，根据
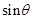∈[0，1]，即可求解．
解：由f（x）=x3+x，∴f（x）为奇函数，增函数，∴f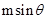（）+f（1-m）＞0恒成立，
即f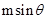（）＞f（m-1），
∴
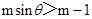，当0≤θ≤
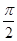时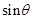，∈[0，1]，
∴
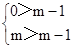，解得m＜1，
故实数m的取值范围是（-∞，1），
故选D．
考查了函数恒成立的问题及函数的奇偶性与单调性，难度较大，关键是先判断函数的奇偶性与单调性．
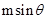＞m-1，根据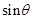∈[0，1]，即可求解．解：由f（x）=x3+x，∴f（x）为奇函数，增函数，∴f（
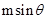）+f（1-m）＞0恒成立，即f（
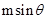）＞f（m-1），∴
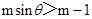，当0≤θ≤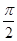时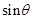，∈[0，1]，∴
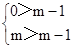，解得m＜1，故实数m的取值范围是（-∞，1），
故选D．
考查了函数恒成立的问题及函数的奇偶性与单调性，难度较大，关键是先判断函数的奇偶性与单调性．
练习册系列答案
相关题目
，函数
．
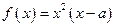在区间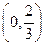
内是减函数，求实数
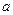的取值范围；
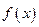在区间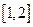
上的最小值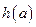
；
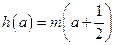有两个不相等的实数解，
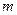的取值范围．
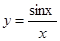在点（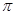
，0）处的切线与直线
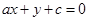垂直，则
= （ ）
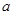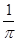
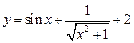在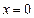
处的切线方程为___________.
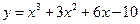的切线中,斜率最小的切线方程是 
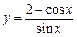在点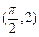
处的切线与直线
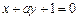垂直，则
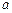等于