题目内容
已知圆C:x2+y2+2x-4y+3=0,若圆C的切线在x轴、y轴上的截距相等,求切线的方程.
切线方程为 或x+y+1=0或x+y-3=0.
或x+y+1=0或x+y-3=0.
解析试题分析:切线在x轴、y轴上的截距相等,可设切线方程为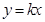 或x+y=a,又根据切线的性质知圆心(-1,2)到切线的距离等于半径
或x+y=a,又根据切线的性质知圆心(-1,2)到切线的距离等于半径 ,由点到直线的距离公式可得
,由点到直线的距离公式可得 与
与 的值.本题中容易遗漏切线为
的值.本题中容易遗漏切线为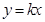 的形式,此时在两坐标轴的距离也相等为
的形式,此时在两坐标轴的距离也相等为 .
.
解: 由方程x2+y2+2x-4y+3=0知圆心为(-1,2),半径为 ,
,
当切线过原点时,设切线方程为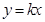 ,则
,则 ,
,
∴ ,即切线方程为
,即切线方程为 .
.
当切线不过原点时,设切线方程为x+y=a,
则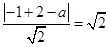 .
.
∴a=-1或a=3,即切线方程为x+y+1=0或x+y-3=0.
∴切线方程为 或x+y+1=0或x+y-3=0.
或x+y+1=0或x+y-3=0.
考点:1.圆的切线的性质;2.点到直线的距离公式;3.直线的截距式方程.

练习册系列答案
相关题目
 与圆C:
与圆C: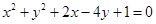 的两个交点,并且面积有最小值,求此圆的方程.
的两个交点,并且面积有最小值,求此圆的方程.
 (
( )
) 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程; 的内部,求实数
的内部,求实数 的取值范围.
的取值范围. ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|. ,求此曲线的方程;
,求此曲线的方程; 的方程为:
的方程为: (
( ,
, 为常数).
为常数). 轴、
轴、 轴交于点
轴交于点 、
、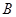 (
( ),试判断
),试判断 的面积
的面积 是否为定值?并证明你的判断;
是否为定值?并证明你的判断; 与曲线
与曲线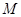 、
、 ,且
,且 ,求曲线
,求曲线 :
:
 ,过定点
,过定点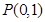 作斜率为1的直线交圆
作斜率为1的直线交圆 、
、 两点,
两点, 为线段
为线段 的中点.
的中点. 的值;
的值; 为圆
为圆 面积的最大值;
面积的最大值; 向圆
向圆 ,且有
,且有 , 求
, 求 的最小值,并求
的最小值,并求 上,点P关于直线
上,点P关于直线 的对称点也在圆C上,则圆C的半径为 .
的对称点也在圆C上,则圆C的半径为 .