题目内容
已知一个圆经过直线l：
与圆C：
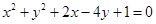的两个交点，并且面积有最小值，求此圆的方程．
解析试题分析：圆面积最小就是圆半径最小，而当以直线与圆交点为直径时所求圆半径最小. 由
解得
或
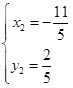，以点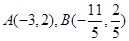
为直径的圆方程为
，化简为
试题解析：解法一：由解得或，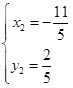
过该两点的圆的面积最小，可求得其方程为
解法二：所求圆的圆心为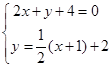
的交点，可求得
，
可求得其方程为
解法三：圆系方程可求得其方程为
考点：圆方程
练习册系列答案
相关题目
题目内容
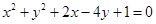已知一个圆经过直线l：与圆C：的两个交点，并且面积有最小值，求此圆的方程．
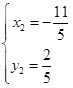解析试题分析：圆面积最小就是圆半径最小，而当以直线与圆交点为直径时所求圆半径最小. 由解得或，以点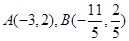为直径的圆方程为，化简为
试题解析：解法一：由解得或，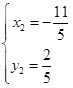
过该两点的圆的面积最小，可求得其方程为
解法二：所求圆的圆心为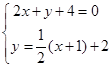的交点，可求得，
可求得其方程为
解法三：圆系方程可求得其方程为
考点：圆方程
，过P点作圆C的两条切线，切点分别为A、B
，直线
,
上一点A的横坐标为
,过点A作圆M的两条切线
,
,切点分别为B,C.
时，求直线
？若存在，求出点A的坐标，若不存在，请说明理由.
，圆
．
被圆
所截得的弦长；
的直线
与直线
垂直，
上的圆
相切，圆
，求圆
的方程化为标准方程，并指出圆心坐标和半径；
被圆
为圆心的圆与直线
相切，过点
的动直线与圆
相交于
两点.
时，求直线
的方程.
的焦点为圆心,且过坐标原点的圆的方程为________________
相切的直线与
轴，
轴的正半轴交于A、B且
，则三角形AOB面积的最小值为 。