题目内容
已知点
，动点P 满足：|PA|=2|PB|．
(1)若点P的轨迹为曲线
，求此曲线的方程；
(2)若点Q在直线l1: x+y+3=0上，直线l2经过点Q且与曲线只有一个公共点M，求|QM|的最小值．
(1) 
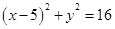;(2) 
．
解析试题分析：(1) 利用两点间距离公式，结合|PA|=2|PB|可求；(2) 由题可知，|QM|=
，当CQ
l1 时，|CQ|取最小值时，|QM|取最小值．
解：（1）设P点的坐标为（x, y）, 由|PA|=2|PB|，得
＝２
,
化简，得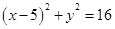,即为所求．
(2)曲线C是以点（5,0）为圆心，4为半径的圆, 直线l2是圆的切线，连接CQ，则
|QM|==
,
当CQl1，|CQ|取最小值，则
．
此时|QM|的最小值为
．
考点：两点间距离公式，直线与圆的位置关系．
练习册系列答案
相关题目
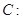
的方程化为标准方程，并指出圆心坐标和半径；
被圆
，求⊙O的半径r的长．
，求圆C方程．
为圆
的直径，
为垂直
，弦
交
.
、
四点共圆；
，求线段
的长. 
为圆心的圆与直线
相切，过点
的动直线与圆
相交于
两点.
时，求直线
的方程.
PO?若存在,指出有几个这样的点;若不存在,请说明理由.
相切的直线与
轴，
轴的正半轴交于A、B且
，则三角形AOB面积的最小值为 。