题目内容
已知曲线 的方程为:
的方程为: (
( ,
, 为常数).
为常数).
(1)判断曲线 的形状;
的形状;
(2)设曲线 分别与
分别与 轴、
轴、 轴交于点
轴交于点 、
、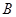 (
( 、
、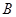 不同于原点
不同于原点 ),试判断
),试判断 的面积
的面积 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线 与曲线
与曲线 交于不同的两点
交于不同的两点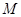 、
、 ,且
,且 ,求曲线
,求曲线 的方程.
的方程.
(1)圆;(2)详见解析;(3) .
.
解析试题分析:(1)在曲线 的方程两边同时除以
的方程两边同时除以 ,并进行配方得到
,并进行配方得到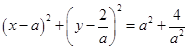 ,从而得到曲线
,从而得到曲线 的具体形状;(2)在曲线
的具体形状;(2)在曲线 的方程中分别令
的方程中分别令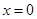 与
与 求出点
求出点 、
、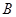 的坐标,再验证
的坐标,再验证 的面积是否为定值;(3)根据条件
的面积是否为定值;(3)根据条件 得到圆心在线段
得到圆心在线段 的垂直平分线上,并且得到圆心与原点
的垂直平分线上,并且得到圆心与原点 的连线与直线
的连线与直线 垂直,利用两条直线斜率乘积为
垂直,利用两条直线斜率乘积为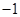 ,求出
,求出 值,并利用直线与圆相交作为检验条件,从而确定曲线
值,并利用直线与圆相交作为检验条件,从而确定曲线 的方程.
的方程.
试题解析:(1)将曲线 的方程化为
的方程化为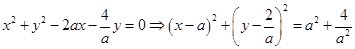 ,
,
可知曲线 是以点
是以点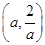 为圆心,以
为圆心,以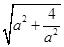 为半径的圆;
为半径的圆;
(2) 的面积
的面积 为定值.
为定值.
证明如下:
在曲线 的方程中令
的方程中令 得
得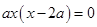 ,得点
,得点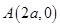 ,
,
在曲线 方程中令
方程中令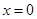 得
得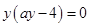 ,得点
,得点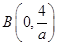 ,
,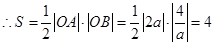 (定值);
(定值);
(3) 圆
圆 过坐标原点,且
过坐标原点,且 ,
, 圆心
圆心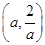 在
在 的垂直平分线上,
的垂直平分线上,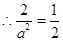 ,
,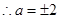 ,
,
当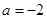 时,圆心坐标为
时,圆心坐标为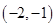 ,圆的半径为
,圆的半径为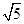 ,
,
圆心到直线 的距离
的距离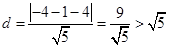 ,
,
直线 与圆
与圆 相离,不合题意舍去,
相离,不合题意舍去,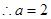 ,这时曲线
,这时曲线 的方程为
的方程为 .
.
考点:1.圆的方程;2.三角形的面积;3.直线与圆的位置关系.

练习册系列答案
相关题目
 ,过P点作圆C的两条切线,切点分别为A、B
,过P点作圆C的两条切线,切点分别为A、B ,求圆C方程.
,求圆C方程. 为圆
为圆 的直径,
的直径, 为垂直
为垂直 ,弦
,弦 交
交 .
. 、
、 四点共圆;
四点共圆; ,求线段
,求线段 的长.
的长. 

 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点 的动直线与圆
的动直线与圆 相交于
相交于 两点.
两点. 时,求直线
时,求直线 的方程.
的方程. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以坐标原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.