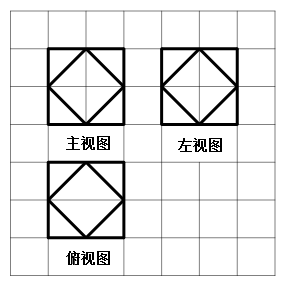
题目内容
【题目】(本小题满分12分)已知椭圆C:![]() 的离心率为
的离心率为![]() ,连接椭圆四个顶点形成的四边形面积为4
,连接椭圆四个顶点形成的四边形面积为4![]() .
.
(1)求椭圆C的标准方程;
(2)过点A(1,0)的直线与椭圆C交于点M, N,设P为椭圆上一点,且![]() O为坐标原点,当
O为坐标原点,当![]() 时,求t的取值范围.
时,求t的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题本题主要考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先利用离心率、![]() 、四边形的面积列出方程,解出a和b的值,从而得到椭圆的标准方程;第二问,讨论直线MN的斜率是否存在,当直线MN的斜率存在时,直线方程与椭圆方程联立,消参,利用韦达定理,得到
、四边形的面积列出方程,解出a和b的值,从而得到椭圆的标准方程;第二问,讨论直线MN的斜率是否存在,当直线MN的斜率存在时,直线方程与椭圆方程联立,消参,利用韦达定理,得到![]() 、
、![]() ,利用
,利用![]() 列出方程,解出
列出方程,解出![]() ,代入到椭圆上,得到
,代入到椭圆上,得到![]() 的值,再利用
的值,再利用![]() ,计算出
,计算出![]() 的范围,代入到
的范围,代入到![]() 的表达式中,得到t的取值范围.
的表达式中,得到t的取值范围.
试题解析:(1)![]() ,
,![]() ,即
,即![]() .
.
又![]() ,
,![]() .
.
∴椭圆C的标准方程为![]() .
.
(2)由题意知,当直线MN斜率存在时,
设直线方程为![]() ,
,![]() ,
,
联立方程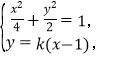 消去y得
消去y得![]() ,
,
因为直线与椭圆交于两点,
所以![]() 恒成立,
恒成立,
![]() ,
,
又![]() ,
,
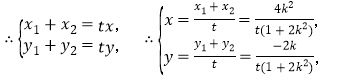
因为点P在椭圆![]() 上,所以
上,所以![]() ,
,
即![]() ,
,
又![]() ,
,
即![]() ,整理得:
,整理得:![]() ,
,
化简得:![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
![]() ,即
,即![]() .
.
当直线MN的斜率不存在时,![]() ,此时
,此时![]() ,
,
![]() .
.

【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查.现在按课外阅读时间的情况将学生分成三类:![]() 类(不参加课外阅读),
类(不参加课外阅读),![]() 类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),
类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),![]() 类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时).调查结果如下表:
|
|
| |
男生 |
| 5 | 3 |
女生 |
| 3 | 3 |
(1)求出表中![]() ,
,![]() 的值;
的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | ||
不参加课外阅读 | ||||
参加课外阅读 | ||||
总计 |
P(K≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |