题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若△![]() 的面积为1(
的面积为1(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)将点![]() 代入椭圆方程得
代入椭圆方程得![]() ,依题意椭圆离心率
,依题意椭圆离心率![]() ,联立方程组解得
,联立方程组解得![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() ;(2)设
;(2)设![]() ,
,![]() ,将直线
,将直线![]() :
:![]() 与椭圆
与椭圆![]() :
:![]() 联立,可得
联立,可得![]() ,写出根与系数关系,利用弦长公式求出
,写出根与系数关系,利用弦长公式求出![]() ,利用点到直线距离公式求得高,利用面积公式建立方程
,利用点到直线距离公式求得高,利用面积公式建立方程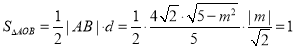 ,解得
,解得![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
试题解析:
(1)∵离心率![]() ,∴
,∴![]() ,即
,即![]() ,得
,得![]() ,①
,①
∵椭圆![]() 经过点
经过点![]() ,∴
,∴![]() ,②
,②
联立①②,解得![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,
将直线![]() :
:![]() 与椭圆
与椭圆![]() :
:![]() 联立,可得
联立,可得![]() .
.
由![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
∴![]()
![]() ,
,
原点![]() 到直线
到直线![]() :
:![]() 的距离
的距离![]() ,
,
∴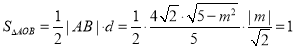 ,
,
化简得,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 |
| 0.1 |
第2组 |
| 0.1 |
第3组 |
| 0.4 |
第4组 |
| 0.3 |
第5组 |
| 0.1 |
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.