Question

【题目】已知，AB为圆O的直径，CD为垂直AB的一条弦，垂足为E，弦AG交CD于F．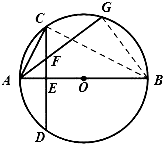

（1）求证：E、F、G、B四点共圆；
（2）若GF=2FA=4，求线段AC的长．

Answer 1

【答案】
（1）证明：如图，连结BG，

由AB为直径可知∠AGB=90°

又CD⊥AB，所以∠BEF=∠AGB=90°，

因此E、F、G、B四点共圆．

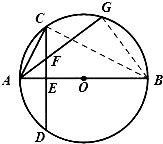
（2）解：连结BC，由E、F、G、B四点共圆，

所以AFAG=AEBA，

在Rt△ABC中，AC2=AEBA，

由于GF=2FA=4，得AF=2，FG=4，即有AG=6，

所以AC2=2×6，

故AC=2

【解析】（1）连结BG，由AB为直径可知∠AGB=90°，又CD⊥AB，由此能证明E、F、G、B四点共圆；（2）连结BC，由E、F、G、B四点共圆，运用切割线定理，得AFAG=AEBA，再由直角三角形ABC中的射影定理，得AC2=AEBA，代入数据，即可求出线段AC的长．