题目内容
【题目】设函数f(x)=ex(ax+b)(其中e=2.71828…),g(x)=x2+2bx+2,已知它们在x=0处有相同的切线.
(1)求函数f(x),g(x)的解析式;
(2)若函数F(x)=f(x)+g(x)﹣2(ex+x),试判断函数F(x)的零点个数,并说明理由;
(3)若函数f(x)在[t,t+1](t>﹣3)上的最小值为φ(t),解关于t的不等式φ(t)≤4e2 .
【答案】
(1)解:∵f(x)=ex(ax+b),g(x)=x2+2bx+2
∴f′(x)=ex(ax+a+b),g′(x)=2x+2b,
由题意它们在x=0处有相同的切线,
∴f′(0)=a+b=g′(0)=2b,∴a=b,
f(0)=b=g(0)=2,∴a=b=2,
∴f(x)=2ex(x+1),g(x)=x2+4x+2
(2)解:由题意F(x)=2xex+x2+2x+2,
∴F′(x)=2(ex+1)(x+1),
由F′(x)>0,得x>﹣1;由F′(x)<0,得x<﹣1,
∴F(x)在(﹣1,+∞)上单调递增,在(﹣∞,﹣1)上单调递减,
∴F(x)极小值=F(﹣1)=1﹣ ![]() >0,
>0,
∴函数F(x)的零点个数为0.
(3)解:f′(x)=2ex(x+2),由f′(x)>0,得x>﹣2,
由f′(x)<0,得x<﹣1,∴F(x)在(﹣2,+∞)单调递增,在(﹣∞,﹣2)单调调递减,
∵t>﹣3,∴t+1>﹣2.
①当﹣3<t<﹣2时,f(x)在(t,﹣2)单调递减,(﹣2,t+1)单调递增,
∴ ![]() .
.
②当t≥﹣2时,f(x)在[t,t+1]单调递增,
∴ ![]()
∴φ(t)= ![]() ,
,
当﹣3<t<﹣2时,φ(t)≤4e2,
当t≥﹣2时,φ(t)=2et(t+1),
当﹣2≤t≤﹣1时,φ(t)≤4e2,
当t>﹣1时,φ(t)=2et(t+1)是增函数,又φ(2)=6e2,
∴﹣1<t≤2,
∴不等式φ(t)≤4e2的解集为(﹣3,2].
【解析】(1)由已知条件得f′(x)=ex(ax+a+b),g′(x)=2x+2b,f′(0)=a+b=g′(0)=2b,f(0)=b=g(0)=2,由此求出a=b=2,从而能求出f(x)=2ex(x+1),g(x)=x2+4x+2.(2)由题意F′(x)=2(ex+1)(x+1),由导数性质得F(x)极小值=F(﹣1)=1﹣ ![]() >0,由此求出函数F(x)的零点个数为0.(3)f′(x)=2ex(x+2),由导数性质求出φ(t)=
>0,由此求出函数F(x)的零点个数为0.(3)f′(x)=2ex(x+2),由导数性质求出φ(t)= ![]() ,由此能示出不等式φ(t)≤4e2的解集.
,由此能示出不等式φ(t)≤4e2的解集.
【考点精析】根据题目的已知条件,利用函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为[80,90)、[90,100)、[100,110)、[110,120)、[120,130),由此得到两个班测试成绩的频率分布直方图: 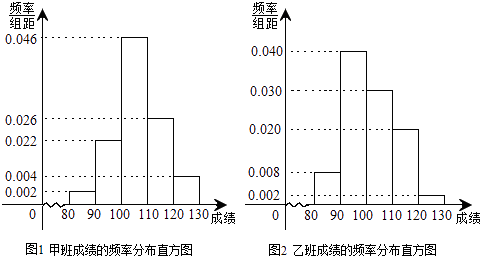
(1)完成下面2×2列联表,你能有97.5%的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 | a= | b= | 50 |
乙班 | c=24 | d=26 | 50 |
合计 | e= | f= | 100 |
(2)现从乙班50人中任意抽取3人,记ξ表示抽到测试成绩在[100,120)的人数,求ξ的分布列和数学期望Eξ.
附:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.204 | 6.635 | 7.879 | 10.828 |