题目内容
(本题满分12分)
已知函数f(x)=x3+ax2+(a+6)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是3,求a,b的值;
(2)若f(x)为R上的单调递增函数,求a的取值范围.
解:(1)由函数f(x)的图象过原点,得b="0," ………………………………1分
又f′(x)=3x2+2ax+(a+6), …………………………………………………3分
f(x)在原点处的切线斜率是3,则a+6=3,所以a="-3." ………………………6分
(2)若f(x)为R上的单调递增函数,则f′(x) 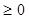 在R上恒成立.
在R上恒成立.
即3x2+2ax+(a+6)≥0在R上恒成立,………………………………………8分
因此Δ≤0,有4a2-12(a+6) ≤0 ………………………………………10分
即a2-3a-18 ≤0解得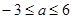 ……………………………………………12分
……………………………………………12分
解析试题分析:(Ⅰ)根据函数f(x)的图象过点P(1,2)与函数图象在点P处的切线斜率为8,建立关于a和b的方程组,解之即可;
(Ⅱ)由(Ⅰ)得f'(x),f(x)为R上的单调递增函数则令f'(x)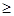 0即可求出a的范围.
0即可求出a的范围.
考点:本试题主要考查了导函数的正负与原函数的单调性之间的关系,以及利用导数研究曲线上某点切线方程等基础知识,同时考查了分析与解决问题的综合能力,属于基础题。
点评:解决该试题的关键对于导数几何意义的运用和单调递增时要满足到导函数恒大于等于零来得到。

练习册系列答案
相关题目
 ,其中
,其中 是自然对数的底数,
是自然对数的底数,
 时,
时, 的单调性。
的单调性。
 ,使
,使 ,在
,在 与
与 时,都取得极值。
时,都取得极值。 的值;
的值; 都有
都有 恒成立,求c的取值范围。
恒成立,求c的取值范围。
 是
是 的一个极值点.
的一个极值点. 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。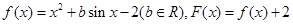 ,且对于任意实数
,且对于任意实数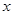 ,恒有
,恒有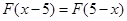 .
. 的解析式;
的解析式;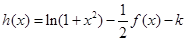 有几个零点?
有几个零点? ,
,
 在
在 处与直线
处与直线 相切;
相切; 的值;②求函数
的值;②求函数 上的最大值;
上的最大值; 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
 的表达式(不需证明);
的表达式(不需证明); 的最大值为
的最大值为 ,
, ,求
,求 的最小值.
的最小值.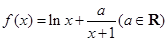 .
.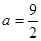 时,求
时,求 的极值;
的极值; 时,试比较
时,试比较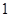 的大小;
的大小;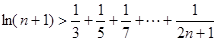 (
(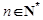 ).
).