题目内容
正实数数列{an}中,a1=1,a2=5,且{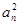 }成等差数列.
}成等差数列.
(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.
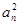 }成等差数列.
}成等差数列.(1)证明:数列{an}中有无穷多项为无理数;
(2)当n为何值时,an为整数?并求出使an<200的所有整数项的和.
(1)见解析 (2)当n=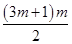 +1(m∈N)和n=
+1(m∈N)和n=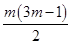 +1(m∈N*)时,an为整数,6733
+1(m∈N*)时,an为整数,6733
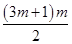 +1(m∈N)和n=
+1(m∈N)和n=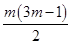 +1(m∈N*)时,an为整数,6733
+1(m∈N*)时,an为整数,6733(1)证明:由已知有:
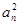 =1+24(n-1),
=1+24(n-1),从而an=
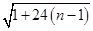 .
.取n-1=242k-1,则an=
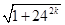 (k∈N*).
(k∈N*).用反证法证明这些an都是无理数.
假设an=
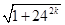 为有理数,则an必为正整数,
为有理数,则an必为正整数,且an>24k,故an-24k≥1,an+24k>1,与(an-24k)(an+24k)=1矛盾,
所以an=
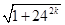 (k∈N*)都是无理数,
(k∈N*)都是无理数,即数列{an}中有无穷多项为无理数.
(2)解:要使an为整数,由(an-1)(an+1)=24(n-1)可知:an-1,an+1同为偶数,且其中一个必为3的倍数,
所以有an-1=6m或an+1=6m.
当an=6m+1时,有
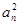 =36m2+12m+1=1+12m(3m+1)(m∈N).
=36m2+12m+1=1+12m(3m+1)(m∈N).又m(3m+1)必为偶数,
所以an=6m+1(m∈N)满足
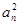 =1+24(n-1),
=1+24(n-1),即n=
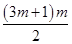 +1(m∈N)时,an为整数;
+1(m∈N)时,an为整数;同理an=6m-1(m∈N*)时,有
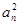 =36m2-12m+1=1+12m(3m-1)(m∈N*)也满足
=36m2-12m+1=1+12m(3m-1)(m∈N*)也满足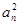 =1+24(n-1),
=1+24(n-1),即n=
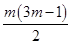 +1(m∈N*)时,an为整数;
+1(m∈N*)时,an为整数;显然an=6m-1(m∈N*)和an=6m+1(m∈N)是数列中的不同项,
所以当n=
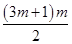 +1(m∈N)和n=
+1(m∈N)和n=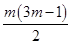 +1(m∈N*)时,an为整数.
+1(m∈N*)时,an为整数.由an=6m+1<200(m∈N)有0≤m≤33,
由an=6m-1<200(m∈N*)有1≤m≤33.
设an中满足an<200的所有整数项的和为S,
则S=(1+7+13+…+199)+(5+11+…+197)=
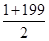 ×34+
×34+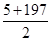 ×33=6733.
×33=6733.
练习册系列答案
相关题目
 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
. ,且该数列前
,且该数列前 最大,求
最大,求 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值; ,则数列
,则数列 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列.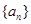 是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。
是公差不为0的等差数列,a1=2且a2,a3,a4+1成等比数列。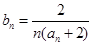 ,求数列
,求数列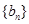 的前
的前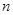 项和
项和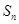
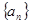
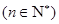 中,其前
中,其前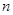 项和为
项和为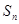 ,满足
,满足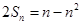 .
.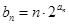 ,求数列
,求数列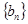 的前
的前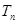 .
.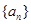 ,
,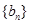 满足:
满足: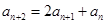 ,
,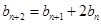 ,
,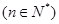 ,那么( )
,那么( )
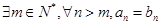


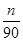 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.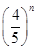 Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由.
Sn,是否存在正整数m,对一切正整数n,总有Tn≤Tm?若存在,求m的值;若不存在,说明理由. 的前
的前 项和为
项和为 ,则
,则