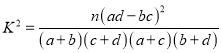题目内容
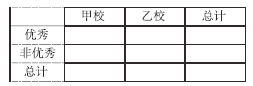
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(Ⅰ)能否据此判断有97.5%的把握认为视觉和空军能力与性别有关?
(Ⅱ)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(Ⅲ)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
【答案】(I)有![]() 的把握认为视觉和空军能力与性别有关;(II)
的把握认为视觉和空军能力与性别有关;(II)![]() ;(III)分布列见解析,
;(III)分布列见解析,![]() .
.
【解析】试题分析:(I)代入公式,计算![]() ,所以有
,所以有![]() 的把握认为有关;(II)将问题转化为线性规划的为题,两者解题事件满足可行域
的把握认为有关;(II)将问题转化为线性规划的为题,两者解题事件满足可行域![]() ,且满足“
,且满足“![]() ”其中甲、乙解答一道几何题的时间分别为
”其中甲、乙解答一道几何题的时间分别为![]() 、
、![]() 分钟.画出可行域,利用几何概型的知识可求得概率为
分钟.画出可行域,利用几何概型的知识可求得概率为![]() ;(III)基本事件的总数为
;(III)基本事件的总数为![]() 种,分别求出甲、乙两人没有一个人被抽到;恰有一人被抽到、两人都被抽到的概率,由此得到分布列和数学期望.
种,分别求出甲、乙两人没有一个人被抽到;恰有一人被抽到、两人都被抽到的概率,由此得到分布列和数学期望.
试题解析:
(Ⅰ)由表中数据得![]() 的观测值
的观测值
![]()
所以根据统计有97.5%的把握认为视觉和空间能力与性别有关.
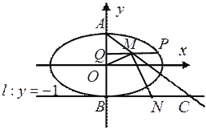
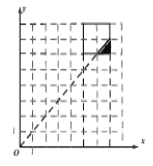
(Ⅱ)设甲、乙解答一道几何题的时间分别为![]() 、
、![]() 分钟,则基本事件满足的区域为
分钟,则基本事件满足的区域为![]() (如图所示)
(如图所示)
设事件![]() 为“乙比甲先做完此道题”则满足的区域为
为“乙比甲先做完此道题”则满足的区域为![]()
![]() 由几何概型
由几何概型![]() 即乙比甲先解答完的概率为
即乙比甲先解答完的概率为![]()
(Ⅲ)由题可知在选择做几何题的8名女生中任意抽取两人,抽取方法有![]() 种,其中甲、乙两人没有一个人被抽到有
种,其中甲、乙两人没有一个人被抽到有![]() 种;恰有一人被抽到有
种;恰有一人被抽到有![]() 种;两人都被抽到有
种;两人都被抽到有![]() 种
种
![]() 可能取值为0,1,2,
可能取值为0,1,2,![]() ,
,
![]() ,
,
![]()
![]() 的分布列为:
的分布列为:
![]() .
.
| 0 | 1 | 2 |
|
|
|
|

 阅读快车系列答案
阅读快车系列答案【题目】已知椭圆![]() 的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为
的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,点
两点,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,若点
,若点![]() 总在以线段
总在以线段![]() 为直径的圆内,求
为直径的圆内,求![]() 的取值范围.
的取值范围.
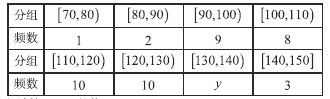
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
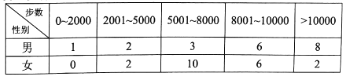
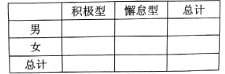
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 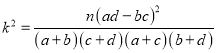 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有![]() 人,超过10000步的有
人,超过10000步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.