题目内容
用反证法证明命题:“已知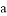 .
.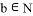 ,若
,若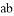 不能被7整除,则
不能被7整除,则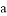 与
与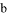 都不能被7整除”时,假设的内容应为( )
都不能被7整除”时,假设的内容应为( )
A. 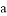 ,
, 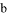 都能被7整除 B.
都能被7整除 B. 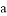 ,
,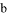 不能被7整除
不能被7整除
C. 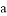 ,
,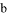 至少有一个能被7整除 D.
至少有一个能被7整除 D. 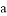 ,
,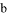 至多有一个能被7整除
至多有一个能被7整除
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
题目内容
用反证法证明命题:“已知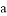 .
.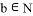 ,若
,若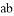 不能被7整除,则
不能被7整除,则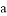 与
与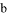 都不能被7整除”时,假设的内容应为( )
都不能被7整除”时,假设的内容应为( )
A. 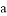 ,
, 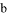 都能被7整除 B.
都能被7整除 B. 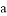 ,
,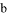 不能被7整除
不能被7整除
C. 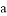 ,
,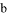 至少有一个能被7整除 D.
至少有一个能被7整除 D. 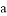 ,
,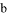 至多有一个能被7整除
至多有一个能被7整除
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案