题目内容
设(1+2i)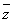 =3-4i(i为虚数单位),则|z|=________.
=3-4i(i为虚数单位),则|z|=________.
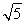
【解析】由已知,|(1+2i)z-|=|3-4i|,
即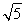 |z-|=5,∴|z|=|z-|=
|z-|=5,∴|z|=|z-|=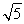

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
题目内容
设(1+2i)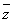 =3-4i(i为虚数单位),则|z|=________.
=3-4i(i为虚数单位),则|z|=________.
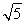
【解析】由已知,|(1+2i)z-|=|3-4i|,
即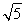 |z-|=5,∴|z|=|z-|=
|z-|=5,∴|z|=|z-|=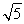

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案