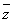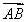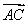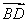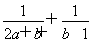题目内容
已知函数f(x)=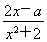 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(1)求实数a的值组成的集合A;
(2)设x1、x2是关于x的方程f(x)=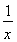 的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
的两个相异实根,若对任意a∈A及t∈[-1,1],不等式m2+tm+1≥|x1-x2|恒成立,求实数m的取值范围.
(1)A={a|-1≤a≤1}(2)(-∞,-2]∪[2,+∞)
【解析】(1)f′(x)=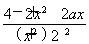 ,
,
因为f(x)在[-1,1]上是增函数,所以当x∈[-1,1]时,
f′(x)≥0恒成立,
令φ(x)=x2-ax-2,即x2-ax-2≤0恒成立.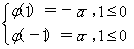 解得-1≤a≤1.
解得-1≤a≤1.
所以A={a|-1≤a≤1}.
(2)由f(x)=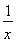 得x2-ax-2=0.
得x2-ax-2=0.
设x1,x2是方程x2-ax-2=0的两个根,所以x1+x2=a,x1x2=-2.从而|x1-x2|=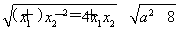 ,因为a∈[-1,1],所以
,因为a∈[-1,1],所以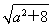 ≤3,即|x1-x2|max=3,
≤3,即|x1-x2|max=3,
不等式对任意a∈A及t∈[-1,1]不等式恒成立,
即m2+tm-2≥0恒成立.
设g(t)=m2+tm-2=mt+m2-2,则
解得m≥2或m≤-2.故m的取值范围是(-∞,-2]∪[2,+∞)

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目