题目内容
)若函数f(x)满足f(x+1)=﹣f(x),且x∈[﹣1,1]时,有f(x)=|x|,则函数y=f(x)﹣1og5|x|零点的个数为 .
考点:
根的存在性及根的个数判断.
专题:
计算题;作图题;函数的性质及应用.
分析:
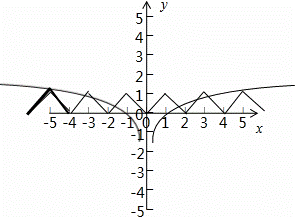
通过函数的性质,画出函数的图象,判断两个函数的图象交点的个数即可.
解答:
解:由f(x+1)=﹣f(x)⇒f(x+2)=f(x),
所以函数的周期是2,因为f(x)和y=1og5|x|都是偶函数,
所以画出两个函数在y轴右侧的图象,找出交点个数即可.
所以函数y=f(x)﹣1og5|x|零点的个数为:8.
故答案为:8.
点评:
本题考查函数零点的个数的求法,数形结合是解答本题的关键.

练习册系列答案
相关题目