题目内容
6.已知函数f(x)=x-lnax,g(x)=$\frac{x}{{e}^{x}}$,其中a≠0,a∈R,e为自然常数.(1)讨论f(x)的单调性和极值;
(2)当a=1时,求使不等式f(x)>mg(x)恒成立的实数m单位取值范围.
分析 (1)先求出函数的定义域,通过讨论a的范围,从而求出函数的单调性、极值问题;
(2)将a=1代入,求出函数f(x)的表达式,函数的导数,得到函数的单调区间,通过讨论m的范围,得到不等式解出即可.
解答 解:(1)∵f(x)=x-lnax,a≠0,a∈R,
∴a>0时,f(x)的定义域为(0,+∞),a<0时,f(x)的定义域为(-∞,0),
又f′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$,
∴a>0时,x>0,f(x)在(0,1)单调递减,在(1,+∞)单调递增,
f(x)有极限值f(1)=1-lna,
a<0时,x<0,f′(x)>0,f(x)在(-∞,0)单调递增,无极值;
(2)当a=1时,f(x)=x-lnx,
由(1)得当且仅当x=1时,f(x)min=1,
∵g′(x)=$\frac{1-x}{{e}^{x}}$,x>0,
∴g(x)在(0,1)单调递增,在(1,+∞)单调递减,
当且仅当x=1时,g(x)max=$\frac{1}{e}$,
当m≤0时,由于g(x)=$\frac{x}{{e}^{x}}$>0,f(x)min=1,
∴f(x)>mg(x)恒成立;
m>0时,[mg(x)]max=$\frac{m}{e}$,要使不等式f(x)>mg(x)恒成立,
只需1>$\frac{m}{e}$,即m<e,
综上,m的范围是(-∞,e).
点评 本题考察了函数的单调性、最值问题,考察了导数的应用,第二问中求出函数的单调区间和最值是解答本题的关键,本题属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(x>-1)}\end{array}\right.$,若f(x)=3,则x的值是( )
| A. | 1 | B. | 1或±$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
1.设AB为半圆O的直径,点C是弧AB的一个三等份点,点D是直径AB的一个三等份点,且点C、D均靠近B点,若半圆O的半径为3,则$\overrightarrow{DC}•\overrightarrow{AB}$=( )
| A. | 0 | B. | $\frac{3}{2}$ | C. | 3 | D. | $\frac{9}{2}\sqrt{3}$ |
11.直线y=kx+b通过第一、三、四象限,则有( )
| A. | d>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
15.已知sinx+cosx=$\sqrt{1+sin2x}$,则x的取值范围是( )
| A. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ](k∈Z) | B. | [$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{4}$+2kπ,$\frac{3π}{4}$+2kπ](k∈Z) | D. | [$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ](k∈Z) |
16.运行如图的程序框图,则输出s的结果是( )
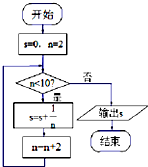

| A. | $\frac{25}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |