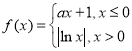题目内容
【题目】方舱医院的启用在本次武汉抗击新冠疫情的关键时刻起到了至关重要的作用,图1为某方舱医院的平面设计图,其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得,图2中所示多边形![]() ,整体设计方案要求:内部井字形的两根水平横轴
,整体设计方案要求:内部井字形的两根水平横轴![]() 米,两根竖轴
米,两根竖轴![]() 米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为
米,记整个方舱医院的外围隔离线(图2实线部分,轴和边框的粗细忽略不计)总长度为![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() 与
与![]() 、
、![]() 的交点为
的交点为![]() 、
、![]() ,
,![]() (
(![]() ).
).

(1)若![]() ,且两根横轴之间的距离
,且两根横轴之间的距离![]() 米,求外围隔离线总长度
米,求外围隔离线总长度![]() ;
;
(2)由于疫情需要,外围隔离线总长度![]() 不超过240米,当整个方舱医院(多边形
不超过240米,当整个方舱医院(多边形![]() 的面积)最大时,给出此设计方案中
的面积)最大时,给出此设计方案中![]() 的大小与
的大小与![]() 的长度.
的长度.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)根据条件,求出外围隔离线每边的长度,再求和即可;
(2)先得到当外围隔离线总长度为240米时,整个方舱医院的面积最大,再将整个方舱医院的面积用![]() 表示出来,观察题中出现
表示出来,观察题中出现![]() 和
和![]() ,可用两者之间的联系化简求最值成立的条件.
,可用两者之间的联系化简求最值成立的条件.
解:(1)由题![]() ,得
,得![]() ,得
,得![]() ,由
,由![]() ,
,
则![]() ,
,![]() ,故
,故![]() ,
,
则![]()
![]()
![]()
![]()
![]()
(2)设![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
则![]()
![]()
![]()
![]()
![]() .
.
当![]() 会使整个方舱医院的面积最大,则
会使整个方舱医院的面积最大,则![]() ,
,
得![]() ,
,
整个方舱医院的面积![]()
![]() ,
,
得![]()
![]() ,
,![]()
令![]()
![]() ,
,![]() ,则
,则![]() ,
,
且![]() ,得
,得![]()
则![]() ,
,![]()
当![]() 时,
时,![]() 最大,即
最大,即![]()
![]() ,此时
,此时![]() ,
,![]() ,
,
即整个方舱医院的面积最大时,![]() ,
,![]()

【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.