题目内容
【题目】已知函数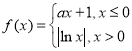 ,给出下列三个结论:
,给出下列三个结论:
①当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ;
;
②若函数![]() 无最小值,则
无最小值,则![]() 的取值范围为
的取值范围为![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ,使得函数
,使得函数![]() .恰有3个零点
.恰有3个零点![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
其中,所有正确结论的序号是______.
【答案】②③
【解析】
由题意结合函数单调性的概念举出反例可判断①;画出函数的图象数形结合即可判断②;由题意结合函数图象不妨设![]() ,进而可得
,进而可得![]() ,
,![]() ,
,![]() ,令
,令![]() 验证后即可判断③;即可得解.
验证后即可判断③;即可得解.
对于①,当![]() 时,由
时,由![]() ,
,![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 不单调递减,故①错误;
不单调递减,故①错误;
对于②,函数 可转化为
可转化为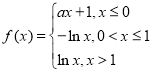 ,
,
画出函数的图象,如图:
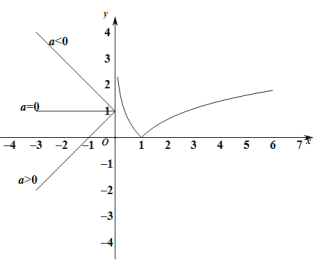
由题意可得若函数![]() 无最小值,则
无最小值,则![]() 的取值范围为
的取值范围为![]() ,故②正确;
,故②正确;
对于③,令![]() 即
即![]() ,结合函数图象不妨设
,结合函数图象不妨设![]() ,
,
则![]() ,
,
所以![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() 即
即![]() ,
,
当![]() 时,
时,![]() ,
,![]() 存在三个零点,且
存在三个零点,且![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,
,![]() 存在三个零点,且
存在三个零点,且![]() ,符合题意;
,符合题意;
故③正确.
故答案为:②③.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某央企在一个社区随机采访男性和女性用户各50名,统计他(她)们一天(![]() )使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
)使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
男性用户的频数分布表
男性用户日用时间分组( |
|
|
|
|
|
频数 | 20 | 12 | 8 | 6 | 4 |
女性用户的频数分布表
女性用户日用时间分组( |
|
|
|
|
|
频数 | 25 | 10 | 6 | 8 | 1 |
(1)分别估计男性用户,女性用户“手机迷”的频率;
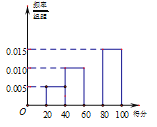
(2)求男性用户每天使用手机所花时间的中位数;
(3)求女性用户每天使用手机所花时间的平均数与标准差(同一组中的数据用该组区间的中点值作代表).