题目内容
【题目】函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:⑴先求出函数的定义域,再求导数![]() ,令
,令![]() ,讨论
,讨论![]() 与0的关系,从而求出函数的单调性⑵若函数
与0的关系,从而求出函数的单调性⑵若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,则必是
,则必是![]() ,得
,得![]() 、
、![]() 是
是![]() 的二根,
的二根,
∴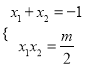 , 给出
, 给出![]() 的关系,下证
的关系,下证![]() ,构造新函数,证明不等式
,构造新函数,证明不等式
解析: ![]() 的定义域是
的定义域是![]() ,
, ![]() ,
,
(1)由题设知, ![]() ,令
,令![]() ,这是开口向上,以
,这是开口向上,以![]() 为对称轴的抛物线,
为对称轴的抛物线, ![]() ,
,
①当![]() ,即
,即![]() 时,
时, ![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
②当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() ,令
,令![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
1)当![]() 即
即![]() 时,
时, ![]() ,故在
,故在![]() 上,
上, ![]() ,即
,即![]() ,在
,在![]() 上,
上, ![]() ,即
,即![]() .
.
2)当![]() 时,即
时,即![]() 时,
时,
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| + | 0 | - | 0 | + |
| 递增 | 递减 | 递增 |
综上:
![]() 时,
时, ![]() 在
在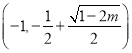 上单调递减,在
上单调递减,在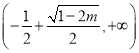 上单调递增;
上单调递增;
![]() 时,
时, ![]() 在
在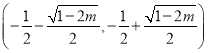 上单调递减,在
上单调递减,在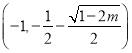 和
和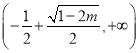 上单调递增;
上单调递增;
![]() 时,
时, ![]() 在
在![]() 上单调递增.
上单调递增.
(2)若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,
,
则必是![]() ,
, ![]() ,则
,则![]() ,
,
且![]() 在
在![]() 上单减,在
上单减,在![]() 和
和![]() 上单增,则
上单增,则![]() ,
,
∵![]() 、
、![]() 是
是![]() 的二根,
的二根,
∴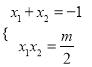 ,即
,即![]() ,
, ![]() ,
,
∴若证![]() 成立,只需证
成立,只需证
![]()
![]()
![]()
![]()
![]() .
.
即证![]()
![]() 对
对![]() 恒成立,
恒成立,
设![]()
![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
故![]() ,故
,故![]() 在
在![]() 上单增,
上单增,
故![]()
![]() ,
,
∴![]()
![]() 对
对![]() 恒成立,
恒成立,
∴![]() .
.

【题目】房产税改革向前推进之路,虽历经坎坷,但步伐从未停歇,作为未来的新增税种,十二届全国人大常委会已将房产税立法正式列入五年立法规划。某市税务机关为了进一步了解民众对政府择机出台房产税的认同情况,随机抽取了一小区住户进行调查,各户人均月收入(单位:千元)的频数分布及赞成出台房产税的户数如下表:
人均月收入 |
|
|
|
|
|
|
频数 | 6 | 10 | 13 | 11 | 8 | 2 |
不赞成户数 | 5 | 9 | 12 | 9 | 4 | 1 |
若将小区人均月收入不低于7.5千元的住户称为“高收入户”,人均月收入低于7.5千元的住户称为“非高收入户”,有![]() 列联表:
列联表:
非高收入户 | 高收入户 | 总计 | |
不赞成 | |||
赞成 | |||
总计 |
(1)根据已知条件完成如图所给的![]() 列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
列联表,并说明能否在犯错误的概率不超过0.005的前提下认为“收入的高低”与“赞成出台房产税”有关.
(2)现从月收入在![]() 的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
的住户中随机抽取两户,求所抽取的两户都不赞成出台房产税的概率;
附:临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() .
.