题目内容

【题目】锐角三角形中， ， ，则面积的取值范围为（ ）

A. B.

C. D.

【答案】B

【解析】∵∠A=30°，BC=1，可得： ∴AB=2sinC，AC=2sinB=2sin（150°-C）=2（cosC+sinC）=cosC+sinC，∴S△ABC= ∵C∈（， ），可得：2C-∈（0， ），∴sin（2C-）∈（0，1]，可得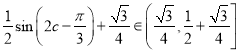： 则△ABC面积的取值范围为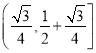

故选B.

点睛: 解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题通法思路是：全部转化为角的关系，建立函数关系式，如，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可.

练习册系列答案
相关题目

【题目】已知椭圆 =1（a＞b＞0）右顶点与右焦点的距离为 ﹣1，短轴长为2 ． （Ⅰ）求椭圆的方程；
（Ⅱ）过左焦点F的直线与椭圆分别交于A、B两点，若△OAB（O为直角坐标原点）的面积为 ，求直线AB的方程．

【题目】选修4﹣1：几何证明选讲
如图，⊙O和⊙O′相交于A，B两点，过A作两圆的切线分别交两圆于C、D两点，连接DB并延长交⊙O于点E．证明：

（1）ACBD=ADAB；
（2）AC=AE．

【题目】已知函数f(x)＝x2＋ax＋b ， g(x)＝ex(cx＋d)，若曲线y＝f(x)和曲线y＝g(x)都过点P(0，2)，且在点P处有相同的切线y＝4x＋2．
（1）求a ， b ， c ， d的值；
（2）若x≥－2时，恒有f(x)≤kg(x)，求k的取值范围．

【题目】如图，在△ABC中，已知A(5，－2)，B(7,3)，且AC边的中点M在y轴上，BC的中点N在x轴上．

(1)求点C的坐标；

(2)求边上的中线所在直线方程．

【题目】已知函数fn（x）= （n∈N*），关于此函数的说法正确的序号是
①fn（x）（n∈N*）为周期函数；②fn（x）（n∈N*）有对称轴；③（ ，0）为fn（x）（n∈N*）的对称中心：④|fn（x）|≤n（n∈N*）．

【题目】函数f（x）＝xlnx－a（x－1）2－x，g（x）＝lnx－2a（x－1），其中常数a∈R．
（Ⅰ）讨论g（x）的单调性；
（Ⅱ）当a＞0时，若f（x）有两个零点x1 ， x2（x1＜x2），求证：在区间（1，＋∞）上存在f（x）的极值点x0 ， 使得x0lnx0＋lnx0－2x0＞0．

【题目】在2015﹣2016赛季CBA联赛中，某队甲、乙两名球员在前10场比赛中投篮命中情况统计如下表（注：表中分数 ，N表示投篮次数，n表示命中次数），假设各场比赛相互独立．

1

2

3

4

5

6

7

8

9

10

甲

乙

根据统计表的信息：
（1）从上述比赛中等可能随机选择一场，求甲球员在该场比赛中投篮命中率大于0.5的概率；
（2）试估计甲、乙两名运动员在下一场比赛中恰有一人命中率超过0.5的概率；
（3）在接下来的3场比赛中，用X表示这3场比赛中乙球员命中率超过0.5的场次，试写出X的分布列，并求X的数学期望．

【题目】如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，

（1）证明：PA∥平面EDB

（2）证明：平面BDE平面PCB

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网