题目内容
函数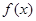 的定义域为R,若
的定义域为R,若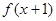 是奇函数,
是奇函数,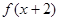 是偶函数. 下列四个结论:
是偶函数. 下列四个结论:
①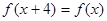 ②
②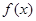 的图像关于点
的图像关于点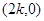 对称
对称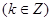
③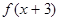 是奇函数 ④
是奇函数 ④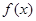 的图像关于直线
的图像关于直线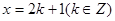 对称
对称
其中正确命题的个数是
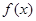 的定义域为R,若
的定义域为R,若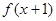 是奇函数,
是奇函数,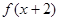 是偶函数. 下列四个结论:
是偶函数. 下列四个结论:①
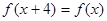 ②
②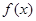 的图像关于点
的图像关于点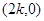 对称
对称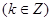
③
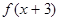 是奇函数 ④
是奇函数 ④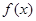 的图像关于直线
的图像关于直线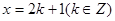 对称
对称其中正确命题的个数是
| A.1 | B.2 | C.3 | D.4 |
B
由题意得:f(-x+1)=-f(x+1).f(-x+2)=f(x+2).所以f[-(x-1)+1]=-f[(x-1)+1]
即f(2-x)=-f(x),因此f(x+2)=-f(x),f[(x+2)+2]=-f(x+2)=-(-f(x))=f(x),
即f(x+4)="f(x)" ①正确;
f(x)图像可由f(x+1)图像右移1个单位得到,f(x+1)图像关于(0,0)对称,则f(x)图像关于点(1,0)对称;②错误;
f(-x+3)=f[2+(1-x)]=f[2-(1-x)]=f(x+1),f(x+3)=f[2+(1+x)]=f[2-(1+x)]=f(-x+1)
所以f(-x+3)=-f(x+3),即f(x+3)是奇函数。③正确;
由f(-x+2)=f(x+2)知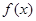 的图像关于直线x=2对称,所以④错误。
的图像关于直线x=2对称,所以④错误。
故选B
即f(2-x)=-f(x),因此f(x+2)=-f(x),f[(x+2)+2]=-f(x+2)=-(-f(x))=f(x),
即f(x+4)="f(x)" ①正确;
f(x)图像可由f(x+1)图像右移1个单位得到,f(x+1)图像关于(0,0)对称,则f(x)图像关于点(1,0)对称;②错误;
f(-x+3)=f[2+(1-x)]=f[2-(1-x)]=f(x+1),f(x+3)=f[2+(1+x)]=f[2-(1+x)]=f(-x+1)
所以f(-x+3)=-f(x+3),即f(x+3)是奇函数。③正确;
由f(-x+2)=f(x+2)知
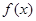 的图像关于直线x=2对称,所以④错误。
的图像关于直线x=2对称,所以④错误。故选B

练习册系列答案
相关题目
 ,使得
,使得



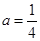 ”是“对任意的正数
”是“对任意的正数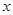 ,均有
,均有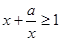 ”的充分非必要条件
”的充分非必要条件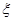 服从正态分布N(2,22),则D(
服从正态分布N(2,22),则D(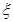 )=2
)=2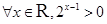 的否定是
的否定是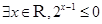
 中,若
中,若 ,则
,则 中,
中, 是
是 的充要条件;
的充要条件; ,则“
,则“ ”是“
”是“ 中,已知
中,已知 ,若点
,若点 在
在 所在的平面内,则
所在的平面内,则 ”的否命题为真命题;
”的否命题为真命题; 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数
为恒均变函数
 ),使sinx+cosx=
),使sinx+cosx=  ;
;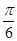 |的最小正周期为p.其中错误的命题为
|的最小正周期为p.其中错误的命题为  若
若 则
则 或
或 ;命题
;命题 :平面内与两个定点
:平面内与两个定点 的距离的和等于常数的点的轨迹叫做椭圆,则下列结论错误的是_______▲___________(填序号)
的距离的和等于常数的点的轨迹叫做椭圆,则下列结论错误的是_______▲___________(填序号) ”为假命题; ②“
”为假命题; ②“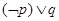 ”为假命题;
”为假命题; ”为真命题; ④“
”为真命题; ④“ ”为真命题.
”为真命题. ,则
,则 ”的逆否命题是
”的逆否命题是  ,则
,则
