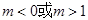题目内容
已知双曲线的中心在原点,离心率为2,一个焦点为F(-2,0).
(1)求双曲线方程;
(2)设Q是双曲线上一点,且过点F,Q的直线l与y轴交于点M,若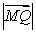 = 2
= 2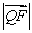 ,求直线l的方程.
,求直线l的方程.
(1)求双曲线方程;
(2)设Q是双曲线上一点,且过点F,Q的直线l与y轴交于点M,若
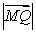 = 2
= 2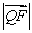 ,求直线l的方程.
,求直线l的方程.(1) 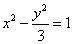
(2)y=±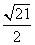 (x+2)或y=±
(x+2)或y=± (x+2)
(x+2)
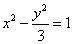
(2)y=±
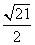 (x+2)或y=±
(x+2)或y=± (x+2)
(x+2)(1)由题意可设所求的双曲线方程为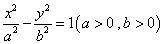 ,
,
则有e=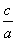 =2,c=2,所以a=1,则b=
=2,c=2,所以a=1,则b=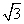 ,
,
所以所求的双曲线方程为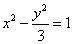 .
.
(2)因为直线l与y轴相交于M且过焦点F(-2,0),
所以l的斜率一定存在,设为k,则l:y=k(x+2),
令x=0,得M(0,2k),
因为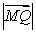 = 2
= 2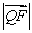 |M,Q,F共线于l,
|M,Q,F共线于l,
所以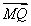 = 2
= 2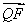 或
或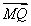 = -2
= -2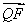
当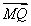 =2
=2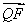 时,
时,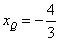 ,
, 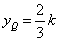 ,
,
所以Q的坐标(-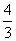 ,
,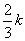 )
)
因为Q在双曲线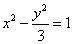 上,
上,
所以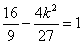 ,所以k=±
,所以k=±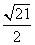 ,
,
所以直线l的方程为y=±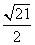 (x+2).
(x+2).
当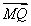 = -2
= -2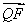 时,
时,
同理求得Q(-4,-2k),代入双曲线方程得,
16-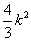 =1,所以k=±
=1,所以k=± ,
,
所以直线l的方程为y=± (x+2).
(x+2).
综上,所求的直线l的方程为y=±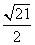 (x+2)或y=±
(x+2)或y=± (x+2).
(x+2).
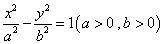 ,
,则有e=
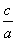 =2,c=2,所以a=1,则b=
=2,c=2,所以a=1,则b=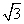 ,
,所以所求的双曲线方程为
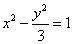 .
.(2)因为直线l与y轴相交于M且过焦点F(-2,0),
所以l的斜率一定存在,设为k,则l:y=k(x+2),
令x=0,得M(0,2k),
因为
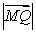 = 2
= 2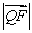 |M,Q,F共线于l,
|M,Q,F共线于l,所以
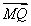 = 2
= 2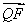 或
或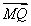 = -2
= -2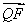
当
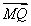 =2
=2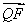 时,
时,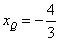 ,
, 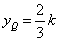 ,
,所以Q的坐标(-
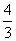 ,
,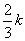 )
)因为Q在双曲线
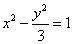 上,
上,所以
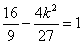 ,所以k=±
,所以k=±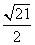 ,
,所以直线l的方程为y=±
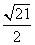 (x+2).
(x+2).当
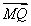 = -2
= -2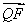 时,
时,同理求得Q(-4,-2k),代入双曲线方程得,
16-
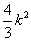 =1,所以k=±
=1,所以k=± ,
,所以直线l的方程为y=±
 (x+2).
(x+2).综上,所求的直线l的方程为y=±
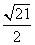 (x+2)或y=±
(x+2)或y=± (x+2).
(x+2).
练习册系列答案
相关题目
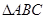 的内切圆与三边
的内切圆与三边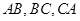 的切点分别为
的切点分别为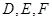 ,已知
,已知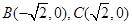 ,内切圆圆心
,内切圆圆心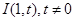 ,设点A的轨迹为R.
,设点A的轨迹为R. 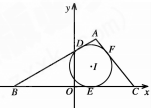
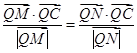 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.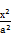 -
-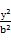 =1的渐近线与圆x2+(y-2)2=1相切,则双曲线离心率为( )
=1的渐近线与圆x2+(y-2)2=1相切,则双曲线离心率为( )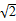
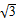
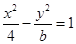 的右焦点为
的右焦点为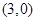 ,则该双曲线的渐近线方程为________.
,则该双曲线的渐近线方程为________. 分别是双曲线C:
分别是双曲线C: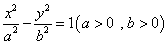 的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )
的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交与点M,若|MF2|=|F1F2|,则C的离心率是( )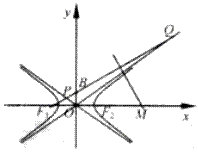
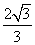
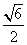
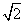
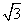
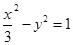 的右准线方程为 ;
的右准线方程为 ;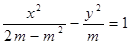 (
(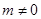 ),若双曲线的离心率
),若双曲线的离心率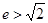 ,则实数m的取值范围是( )
,则实数m的取值范围是( )