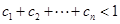题目内容
设 ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列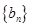 的前
的前 项和为
项和为 ,求
,求 .
.
(1)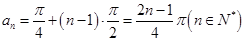 ;(2)
;(2)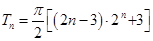 .
.
解析试题分析:(1)先化简 ,得
,得 ,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列
,再根据三角函数的性质找到极值点,利用等差数列的性质写出数列 的通项公式;(2)先根据(1)中的结果写出
的通项公式;(2)先根据(1)中的结果写出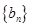 的通项公式,然后写出
的通项公式,然后写出 的解析式,再构造出
的解析式,再构造出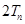 ,利用错位相减法求
,利用错位相减法求 .
.
试题解析:(1) ,其极值点为
,其极值点为 , 2分
, 2分
它在 内的全部极值点构成以
内的全部极值点构成以 为首项,
为首项,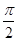 为公差的等差数列, 4分
为公差的等差数列, 4分
所以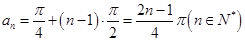 ; 6分
; 6分
(2)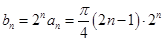 , 8分
, 8分
所以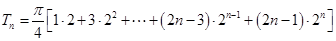 ,
,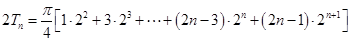 ,
,
相减,得 ,
,
所以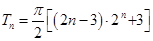 . 12分
. 12分
考点:1、三角函数的恒等变换及化简;2、三角函数的性质的应用;3、等差数列的通项公式;4、错位相减法求数列的前 项和;5、等比数列的前
项和;5、等比数列的前 项和.
项和.

练习册系列答案
相关题目
 满足前
满足前 项和
项和 .
. 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 ,
, .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 .
. 满足
满足 ,
, (
( 且
且 ).
). ;
; ,记数列
,记数列 的前
的前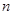 项和为
项和为 ,若
,若 恒为一个与
恒为一个与 ,试求常数
,试求常数 和
和 }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.  求数列
求数列 的前
的前 项和
项和 .
.

 的通项公式;
的通项公式; 求数列
求数列 的前
的前 项和
项和 。
。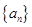 中,已知
中,已知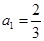 ,
,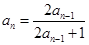 .
.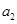 、
、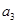 并判断
并判断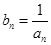 ,求证:
,求证: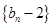 为等比数列;
为等比数列;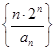 的前n项和
的前n项和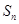 .
. }的前n项和为
}的前n项和为 ,
, ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 项和
项和 ;
; ,
, .求不超过
.求不超过 的最大整数的值。
的最大整数的值。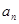 }中,
}中,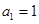 ,
,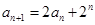 ,设
,设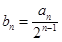 ,
,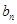 }是等差数列;
}是等差数列;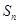 ;
;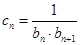 ,证明:
,证明: