题目内容
数列{ }的前n项和为
}的前n项和为 ,
, ,
, .
.
(1)设 ,证明:数列
,证明:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,
, .求不超过
.求不超过 的最大整数的值。
的最大整数的值。
(1)根据题意,得到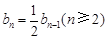 递推关系,进而得到证明。
递推关系,进而得到证明。
(2)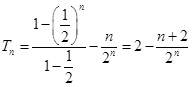
(3)不超过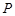 的最大整数为
的最大整数为 .
.
解析试题分析:(1) 因为 ,
,
所以 ① 当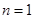 时,
时,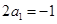 ,则
,则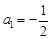 , 1分
, 1分
② 当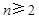 时,
时, , 2分
, 2分
所以 ,即
,即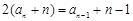 ,
,
所以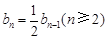 ,而
,而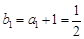 , 4分
, 4分
所以数列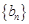 是首项为
是首项为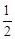 ,公比为
,公比为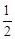 的等比数列,所以
的等比数列,所以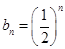 . 5分
. 5分
(2)由(1)得 .
.
所以 ①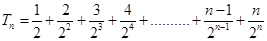 ,
,
②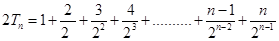 , 7分
, 7分
②-①得: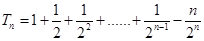 , 8分
, 8分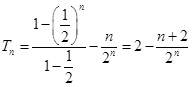 . 10分
. 10分
(3)由(1)知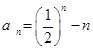
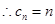 11分
11分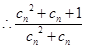
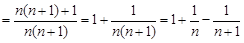 , 13分
, 13分
所以
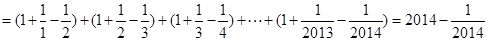 ,
,
故不超过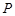 的最大整数为
的最大整数为 . 14分
. 14分
考点:数列的概念和求和的运用
点评:主要是考查了数列的概念,以及数列的求和的运用,属于中档题。

练习册系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示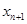 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前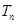 ,求
,求 ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
. ,数列
,数列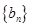 的前
的前 项和为
项和为 ,求
,求 的前
的前 项和为
项和为 ,
, .
. ,证明:数列
,证明:数列 是等比数列;
是等比数列; 的前
的前 .
.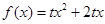
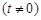
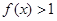 的解集;
的解集;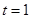 ,记
,记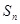 为数列
为数列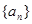 的前
的前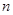 项和,且
项和,且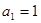 ,
,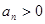
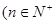 ),点
),点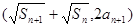 在函数
在函数 的图像上,求
的图像上,求 的前
的前 项和为
项和为 ,已知
,已知 ,求
,求 和
和 是等差数列,且
是等差数列,且 ,
, .
.
 ,求数列
,求数列 的前
的前 项和.
项和.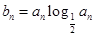 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.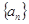 中,已知
中,已知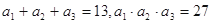 ,且公比为正整数.
,且公比为正整数. 的通项公式;(5分)
的通项公式;(5分) 项和.(5分)
项和.(5分)