题目内容
7．利用对数求导法求下列函数的导数．（1）y=（lnx）x（x＞1）；
（2）y=$\sqrt{\frac{（x+1）（2x-1）}{（x+3）（5x+2）}}$（x＞$\frac{1}{2}$）．
分析 （1）（2）对等式两边取对数，两边求导即可得出．
解答 解：（1）∵y=（lnx）x（x＞1），两边取对数，可得lny=xln（lnx），∴$\frac{1}{y}•{y}^{′}$=ln（lnx）+$\frac{1}{lnx}$，∴y′=（lnx）x$[ln（lnx）+\frac{1}{lnx}]$；
（2）∵y=$\sqrt{\frac{（x+1）（2x-1）}{（x+3）（5x+2）}}$（x＞$\frac{1}{2}$）．
两边取对数可得：lny=$\frac{1}{2}[ln（x+1）+ln（2x-1）-ln（x+3）-ln（5x+2）]$，
∴$\frac{1}{y}•{y}^{′}$=$\frac{1}{2}（\frac{1}{x+1}+\frac{2}{2x-1}-\frac{1}{x+3}-\frac{5}{5x+2}）$，
∴y′=$\sqrt{\frac{（x+1）（2x-1）}{（x+3）（5x+2）}}$•$\frac{1}{2}（\frac{1}{x+1}+\frac{2}{2x-1}-\frac{1}{x+3}-\frac{5}{5x+2}）$，
点评 本题考查了利用对数求导法求导数，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
15．设数列{an}的首项为1，对所有的n≥2，此数列的前n项之积为n2，则这个数列的第3项与第5项的和是（ ）
| A． | $\frac{25}{9}$ | B． | $\frac{21}{25}$ | C． | $\frac{61}{16}$ | D． | $\frac{126}{275}$ |
2．某射手有4发子弹，射击一次命中目标的概率为0.9，如果命中就停止射击，否则一直到子弹用尽，用ξ表示用的子弹数，则P（ξ=4）等于（ ）
| A． | 0.0009 | B． | 0.001 | C． | 0.009 | D． | 以上都不对 |
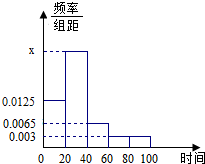某学校随机抽取部分新生调查其上学路上所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学路上所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]．
扣人心弦的2014巴西足球世界杯已落下了帷幕，德国战车再次举起大力神杯，某市足协为了解市民对该届世界杯的关注度，针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查，以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图，如图所示．将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．