题目内容
15.设数列{an}的首项为1,对所有的n≥2,此数列的前n项之积为n2,则这个数列的第3项与第5项的和是( )| A. | $\frac{25}{9}$ | B. | $\frac{21}{25}$ | C. | $\frac{61}{16}$ | D. | $\frac{126}{275}$ |
分析 由题意可得:n≥2时,a1a2•…•an=n2,a1•a2•…•an-1=(n-1)2,可得${a}_{n}=\frac{{n}^{2}}{(n-1)^{2}}$,即可得出.
解答 解:由题意可得:n≥2时,a1a2•…•an=n2,a1•a2•…•an-1=(n-1)2,
∴${a}_{n}=\frac{{n}^{2}}{(n-1)^{2}}$,
∴a2=4,a3=$\frac{9}{4}$,a4=$\frac{16}{9}$,${a}_{5}=\frac{25}{16}$,
∴a3+a5=$\frac{9}{4}+\frac{25}{16}$=$\frac{61}{16}$.
故选:C.
点评 本题考查了递推关系的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
3.设a1,b1,c1,a2,b2,c2均为非零实数,又设不等式a1x2+b1x+c1>0和不等式a2x2+b2x+c2>0的解集分别为M和N,如果$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$=$\frac{{c}_{1}}{{c}_{2}}$,则( )
| A. | M=N | B. | M?N | ||
| C. | M⊆N | D. | 以上答案均不正确 |
10.下列等式不成立的是( )
| A. | log34=$\frac{lg4}{lg3}$ | B. | log34=$\frac{ln4}{ln3}$ | ||
| C. | log34=$\frac{1}{lo{g}_{4}3}$ | D. | log34=$\frac{lo{g}_{1}4}{lo{g}_{1}3}$ |
15.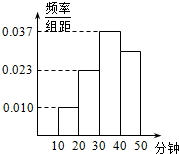 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )| A. | 180 | B. | 450 | C. | 360 | D. | 270 |