题目内容
7.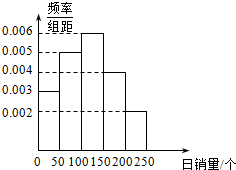 扣人心弦的2014巴西足球世界杯已落下了帷幕,德国战车再次举起大力神杯,某市足协为了解市民对该届世界杯的关注度,针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查,以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
扣人心弦的2014巴西足球世界杯已落下了帷幕,德国战车再次举起大力神杯,某市足协为了解市民对该届世界杯的关注度,针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查,以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.(1)估计日销售量的众数;
(2)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(3)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
分析 (1)直接利用频率分布直方图,估计日销售量的众数即可;
(2)求出“日销售量不低于100个”,“日销售量低于50个”的概率,然后求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(3)推出X的可能值,分别求出X的概率,即可求随机变量X的分布列,利用公式求解数学期望E(X)及方差D(X).
解答 解:(1)依据日销售量的频率分布直方图可得众数为$\frac{100+150}{2}=125$.
(2)记事件A1:“日销售量不低于100个”,事件A2:“日销售量低于50个”,
事件B:“在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个”.
则P(A1)=(0.006+0.004+0.002)×50=0.6,P(A2)=0.003×50=0.15,
P(B)=0.6×0.6×0.15×2=0.108;
(3)X的可能取值为0,1,2,3.
$P(X=0)={C}_{3}^{0}{(1-0.6)}^{3}=0.064$,
$P(X=1)={C}_{3}^{1}×0.6×{(1-0.6)}^{2}=0.288$,
$P(X=2)={C}_{3}^{2}×{0.6}^{2}×(1-0.6)=0.432$,$P(X=3)={C}_{3}^{3}×{0.6}^{3}=0.216$
X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
方差D(X)=3×0.6×(1-0.6)=0.72
点评 解决好离散型随机变量的期望和方差要注意首先要读懂题意,从具体的问题情境中抽象出相应的数学模型,如二项分布,超几何分布,独立事件,古典概型等,要做到运算稳,准,狠.

练习册系列答案
相关题目
15.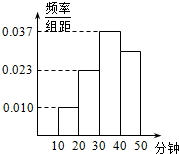 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
 某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )
某健康协会从某地区睡前看手机的居民中随机选取了n人进行调查,得到如图所示的频率分布直方图.已知睡前看手机时间不低于20分钟的有243人,则n的值为( )| A. | 180 | B. | 450 | C. | 360 | D. | 270 |
2.已知m为实数,且sinα,cosα是关于x的方程3x2-mx+1=0的两根,则sin4α+cos4α的值为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
19.在如图的程序框图中,若输入的值为2,则输出的值为( )
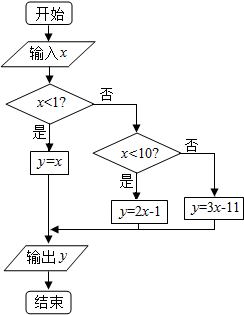

| A. | 2 | B. | 3 | C. | -5 | D. | 6 |
17.在区间[-2,1]任取两个实数x,y,则x+y>0概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{9}$ |