题目内容
15.已知Sn为正项的数列{an}的前n项和,且an+12-an+1+2-an2=0,S29=a292,则以a1为首项,2为公比的等比数列{bn}的第2015项为22017.分析 通过an+12-an+1+2=an2,写出当n从1到29时的28个表达式并相加,利用S29=a292及an>0,可得a1=8,进而可得结论.
解答 解:由已知an>0,
又∵an+12-an+1+2-an2=0,
∴${{a}_{2}}^{2}-{a}_{2}+2={{a}_{1}}^{2}$,
${{a}_{3}}^{2}-{a}_{3}+2={{a}_{2}}^{2}$,
…
${{a}_{29}}^{2}-{a}_{29}+2={{a}_{28}}^{2}$,
将以上28个式子相加,化简得
${{a}_{29}}^{2}$-(S29-a1)+2×28=${{a}_{1}}^{2}$,
又S29=a292,代入上式化简得
(a1-8)(a1+7)=0,
又∵an>0,∴a1=8,
∴b2015=a1•q2015-1=8•22014=22017,
故答案为:22017.
点评 本题考查求数列的通项,利用累加法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
5.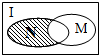 设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
 设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )
设全集是实数集R,M={x|x>2}与N={x|1<x≤3}都是R的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x≤2} | B. | {x|x<2} | C. | {x|-2≤x<1} | D. | {x|-2≤x≤2} |
6.设函数f(x)=$sin(2x+\frac{π}{3})$的图象为M,下面结论中正确的是( )
| A. | 图象M可由y=sin2x的图象向左平移$\frac{π}{6}$个单位得到 | |
| B. | 函数f(x)的最小正周期是4π | |
| C. | 图象M关于直线x=$\frac{π}{3}$对称 | |
| D. | 函数y=f(x)在区间$(-\frac{5π}{6},\frac{π}{6})$上是增函数 |
3.在菱形ABCD中,∠BAD=60°,AB=4,点F是对角线BD上的动点,则$\overrightarrow{AF}$•$\overrightarrow{BF}$的最小值是( )
| A. | -3 | B. | -2 | C. | -$\frac{3}{2}$ | D. | -1 |
10.已知命题p:“将函数y=sin(2x+θ)的图象沿x轴向右平移$\frac{π}{16}$个单位后,得到一个关于y轴对称的图象”,命题q“θ=kπ+$\frac{5π}{8}$(k∈Z)“,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.已知集合A={x|y=$\sqrt{\frac{x-1}{x-4}}$},B={y|y=$\sqrt{16-{2}^{x}}$},则A∩B=( )
| A. | [1,4] | B. | [1,4) | C. | [0,1] | D. | (0,4) |
7.已知函数f(x)=x+1(0≤x≤1),g(x)=2x-$\frac{1}{2}$(x≥1),函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,若方程h(x)-k=0,k∈[$\frac{3}{2}$,2)有两个不同的实根m,n(m>n≥0),则n•g(m)的取值范围为( )
| A. | [$\frac{3}{2}$,2) | B. | [$\frac{1}{4}$,2) | C. | [$\frac{3}{4}$,3] | D. | [$\frac{3}{4}$,2) |