题目内容
7.已知函数f(x)=x+1(0≤x≤1),g(x)=2x-$\frac{1}{2}$(x≥1),函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,若方程h(x)-k=0,k∈[$\frac{3}{2}$,2)有两个不同的实根m,n(m>n≥0),则n•g(m)的取值范围为( )| A. | [$\frac{3}{2}$,2) | B. | [$\frac{1}{4}$,2) | C. | [$\frac{3}{4}$,3] | D. | [$\frac{3}{4}$,2) |
分析 画出函数的图象,利用图象结合已知条件,推出n•g(m)的取值范围即可.
解答 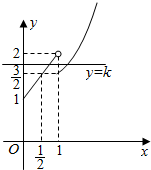 解:函数f(x)=x+1(0≤x≤1),g(x)=2x-$\frac{1}{2}$(x≥1),作出函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,的图象,
解:函数f(x)=x+1(0≤x≤1),g(x)=2x-$\frac{1}{2}$(x≥1),作出函数h(x)=$\left\{\begin{array}{l}{f(x),0≤x<1}\\{g(x),x≥1}\end{array}\right.$,的图象,
若方程h(x)-k=0,k∈[$\frac{3}{2}$,2)有两个不同的实根m,n(m>n≥0),则:$\frac{1}{2}≤n<1$,
ng(m)=nf(n)=n(n+1)=n2+n=(n+$\frac{1}{2}$)2-$\frac{1}{4}$∴$\frac{3}{4}≤ng(m)<2$.
故选:D.
点评 本题考查函数与方程的综合应用,一次函数二次函数指数函数的值域等知识,作出函数的图象是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2. 如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )
如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )
 如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )
如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
 如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值;④点C到线段EF的最大距离为$\sqrt{2}$.
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值;④点C到线段EF的最大距离为$\sqrt{2}$.
