题目内容
8.若实数x,y满足$\left\{\begin{array}{l}{x-2y+2<0}\\{x>0}\\{y<2}\end{array}\right.$,则$\frac{y}{x-1}$的取值范围为( )| A. | (-∞,-1)∪(2,+∞) | B. | (-∞,-1)∪(0,2) | C. | (-1,0)∪(0,2) | D. | (-1,2) |
分析 作出可行域,目标函数z=$\frac{y}{x-1}$表示可行域内的点与A(1,0)连线的斜率,由斜率公式结合图象可得.
解答 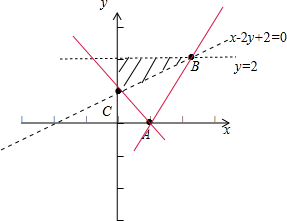 解:作出$\left\{\begin{array}{l}{x-2y+2<0}\\{x>0}\\{y<2}\end{array}\right.$所对应的可行域(如图阴影),
解:作出$\left\{\begin{array}{l}{x-2y+2<0}\\{x>0}\\{y<2}\end{array}\right.$所对应的可行域(如图阴影),
目标函数z=$\frac{y}{x-1}$表示可行域内的点与A(1,0)连线的斜率,
又可得B(2,2),C(0,1),
由斜率公式可得kAB=$\frac{2-0}{2-1}$=2,kAC=$\frac{1-0}{0-1}$=-1,
∴$\frac{y}{x-1}$的取值范围为:(-∞,-1)∪(2,+∞)
故选:A
点评 本题考查简单线性规划,涉及直线的斜率公式,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目
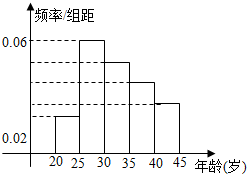 某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )
某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )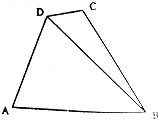 随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°
随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°