题目内容
20.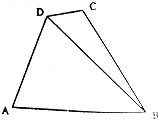 随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°
随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°(Ⅰ)求公路BD的长度;
(Ⅱ)求公路BC的长度.
分析 (1)利用余弦定理只要解三角形ABD即可;
(2)利用正弦定理解三角形BCD.
解答 解:(Ⅰ)在△ABD中,设BD=x,则AB2=BD2+AD2-2BD•AD•cos∠BDA,
即72=52+x2-10xcos60°,整理得到x2-5x-24=0,解得x=8,x=-3(舍去),
所以公路BD的长度为8km;
(Ⅱ)在△BCD中,由正弦定理得到$\frac{BD}{sin∠BCD}=\frac{BC}{sin∠BDC}$,其中BD=8,∠BDC=∠ADC-∠ADB=105°-60°=45°,∠BCD=180°-∠CBD-∠BDC=180°-15°-45°=120°,
所以$\frac{8}{sin120°}=\frac{BC}{sin4{5°}^{\;}}$,所以BC=$\frac{8\sqrt{6}}{3}$,所以公路BC的长度为$\frac{8\sqrt{6}}{3}$km.
点评 本题考查了解三角形的实际应用;关键是将所求转化为解三角形的问题解答.

练习册系列答案
相关题目
11.已知sin(x+$\frac{π}{6}$)=$\frac{1}{4}$,则sin($\frac{5}{6}$π-x)的值为( )
| A. | -$\frac{\sqrt{15}}{4}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
8.若实数x,y满足$\left\{\begin{array}{l}{x-2y+2<0}\\{x>0}\\{y<2}\end{array}\right.$,则$\frac{y}{x-1}$的取值范围为( )
| A. | (-∞,-1)∪(2,+∞) | B. | (-∞,-1)∪(0,2) | C. | (-1,0)∪(0,2) | D. | (-1,2) |
15.已知集合A={x||x-2|>1},B={x|x2+px+q>0},若A=B,则p+q=( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
5.若不等式ax2+bx-1<0的解集为{x|-1<x<2},则a+b=( )
| A. | 6 | B. | 4 | C. | 2 | D. | 0 |
12.已知下列不等式①x2-4x+3<0;②x2-6x+8<0;③2x2-9x+a<0,且使不等式①②成立的x也满足③,则实数a的取值范围是( )
| A. | a≥$\frac{9}{4}$ | B. | a≤10 | C. | a≤9 | D. | a≥-4 |
10.把$y=sin(2x+\frac{π}{3})$的图象向右平移$\frac{π}{6}$个单位,这时图象所表示的函数为( )
| A. | $y=sin(2x+\frac{π}{2})$ | B. | $y=sin(2x+\frac{π}{6})$ | C. | $y=sin(2x+\frac{2π}{3})$ | D. | y=sin2x |