题目内容
【题目】若函数f（x）=x2﹣2ax+3为定义在[﹣2，2]上的函数．
（1）当a=1时，求f（x）的最大值与最小值；
（2）若f（x）的最大值为M，最小值为m，函数g（a）=M﹣m，求g（a）的解析式，并求其最小值．
【答案】
（1）解：当a=1时，f（x）=x2﹣2x+3的对称轴为x=1，
∴f（x）在[﹣2，1]上单调递减，在（1，2]上单调递增，
∴f（x）max=f（﹣2）=4+4+3=11，f（x）min=f（1）=1﹣2+3=2
（2）解：∵f（x）=x2﹣2ax+3的对称轴为x=a，
当a≤﹣2时，f（x）在[﹣2，2]上单调递增，
∴f（x）min=f（﹣2）=4+4a+3=4a+7，f（x）max=f（2）=﹣4a+7，
∴g（a）=M﹣m=﹣4a+7﹣4a﹣7=﹣8a，
当a≥2时，f（x）在[﹣2，2]上单调递减，
∴f（x）max=f（﹣2）=4a+7，f（x）min=f（2）=﹣4a+7，
∴g（a）=M﹣m=4a+7﹣4a﹣7=8a，
当﹣2≤a＜0时，f（x）在[﹣2，a）上单调递减，在（a，2]上单调递增，
∴f（x）max=f（2）=﹣4a+7，f（x）min=f（a）=﹣a2+3，
∴g（a）=M﹣m=﹣4a+a2+3，
当0≤a＜2时，f（x）在[﹣2，a）上单调递减，在（a，2]上单调递增，
∴f（x）max=f（﹣2）=4a+7，f（x）min=f（a）=﹣a2+3，
∴g（a）=M﹣m=4a+a2+3，
∴g（a）=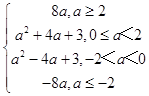 
当a≥2，g（a）min=16，
当0≤a＜2时，g（a）min=g（0）=3，
当﹣2＜a＜0时，g（a）min=g（0）=3，
当a≤﹣2时，g（a）min=16，
综上所述g（a）min=3
【解析】（1）根据二次函数的性质即可求出函数的最值，（2）需要分类讨论，根据对称轴和函数的单调性即可求出最值，即可求出g（a）的解析式，再分别求出最小值，即可得到答案．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减．
