题目内容
【题目】设函数![]() ,若对于在定义域内存在实数
,若对于在定义域内存在实数![]() 满足
满足![]() ,则称函数
,则称函数![]() 为“局部奇函数”.若函数
为“局部奇函数”.若函数![]() 是定义在
是定义在![]() 上的“局部奇函数”,则实数
上的“局部奇函数”,则实数![]() 的取值范围是( )
的取值范围是( )
A. [1﹣![]() ,1+
,1+![]() ) B. [﹣1,2] C. [﹣2
) B. [﹣1,2] C. [﹣2![]() ,2
,2![]() ] D. [﹣2
] D. [﹣2![]() ,1﹣
,1﹣![]() ]
]
【答案】B
【解析】根据“局部奇函数”的定义可知,函数f(﹣x)=﹣f(x)有解即可,
即f(﹣x)=4﹣x﹣m2﹣x+m2﹣3=﹣(4x﹣m2x+m2﹣3),
∴4x+4﹣x﹣m(2x+2﹣x)+2m2﹣6=0,
即(2x+2﹣x)2﹣m(2x+2﹣x)+2m2﹣8=0有解即可.
设t=2x+2﹣x,则t=2x+2﹣x≥2,
∴方程等价为t2﹣mt+2m2﹣8=0在t≥2时有解,
设g(t)=t2﹣mt+2m2﹣8,对称轴x=![]() ,
,
①若m≥4,则△=m2﹣4(2m2﹣8)≥0,
即7m2≤32,此时m不存在;
②若m<4,要使t2﹣mt+2m2﹣8=0在t≥2时有解,
则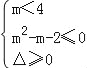 ,解得﹣1≤m<2,综上:﹣1≤m≤2,故选B
,解得﹣1≤m<2,综上:﹣1≤m≤2,故选B

练习册系列答案
相关题目