题目内容
【题目】异面直线a，b成60°，直线c⊥a，则直线b与c所成的角的范围为 ．
【答案】[30°，90°]
【解析】解：如图
作b的平行线b′，交a于O点，
所有与a垂直的直线平移到O点组成一个与直线a垂直的平面α，O点是直线a与平面α的交点，
在直线b′上取一点P，作垂线PP'⊥平面α，交平面α于P'，
∠POP'是b′与面α的线面夹角，∠POP'=30°．
在平面α中，所有与OP'平行的线与b′的夹角都是30°．
在平面α所有与OP'垂直的线
∵PP'⊥平面α，∴该线⊥PP′，
则该线⊥平面OPP'，∴该线⊥b'，与b'的夹角为90°，
与OP'夹角大于0°，小于90°的线，
与b'的夹角为锐角且大于30°．
∴直线b与c所成的角的范围[30°，90°]．
所以答案是：[30°，90°]．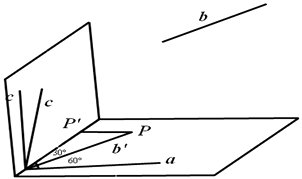
【考点精析】认真审题，首先需要了解异面直线及其所成的角(异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系)．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
