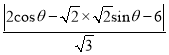题目内容
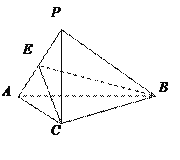
【题目】 如图,在三棱锥
如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求证![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)略,(Ⅱ) ![]() ,(Ⅲ)
,(Ⅲ)![]()
【解析】 解法一
解法一
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)![]() ,
, ![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
, ![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
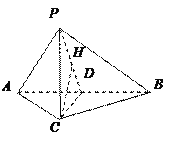
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 的长即为点
的长即为点![]() 到平面
到平面![]() 的距离.
的距离.
由(Ⅰ)知![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二
(Ⅰ)![]() ,
, ![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
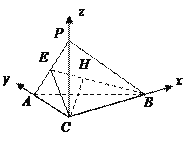
(Ⅱ)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
 则
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
, ![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
, ![]() ,
, ![]() ,
,
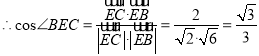 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)![]() ,
,
![]() 在平面
在平面![]() 内的射影为正
内的射影为正![]() 的中心
的中心![]() ,且
,且![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系![]() .
.
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
相关题目