题目内容
【题目】在平面直角坐标系xOy中，已知圆C的方程为
，点
．
求过点M且与圆C相切的直线方程；
过点M任作一条直线与圆C交于A，B两点，圆C与x轴正半轴的交点为P，求证：直线PA与PB的斜率之和为定值．
【答案】（1）
，或
；（2）见解析
【解析】
（1）显然直线l的斜率不存在时，与圆相切，直线l的斜率存在时，设切线方程为y+3=k（x﹣2），利用圆心到直线的距离等于半径，即可求过点P（2，﹣3）且与圆C相切的直线l的方程；
（2）设出AB的方程，代入圆的方程，转化为根与系数之间的关系，利用设而不求思想结合直线斜率进行整理即可．
当直线l的斜率不存在时，显然直线与圆相切，
当直线l的斜率存在时，设切线方程为
，
圆心到直线的距离等于半径，
，解得
，切线方程为：
即过点
且与圆C相切的直线l的方程；，或．
依题意可得当直线AB的斜率存在且不为0时，设直线AB：，代入
，
整理得
；
设
，
，又
，
，
，
直线PA与PB的斜率之和为
，
，
，
，
，
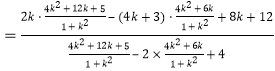为定值．
练习册系列答案
相关题目
【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x/万件 | 10 | 11 | 13 | 12 | 8 | 6 |
利润y/万元 | 22 | 25 | 29 | 26 | 16 | 12 |
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程
x+
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
