题目内容
(本小题满分14分)
已知数列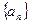 的前
的前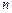 项和为
项和为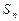 ,若
,若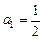 且
且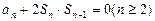 .
.
(Ⅰ)求证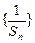 是等差数列,并求出
是等差数列,并求出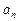 的表达式;
的表达式;
(Ⅱ)若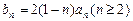 ,求证
,求证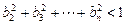 .
.
已知数列
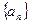 的前
的前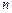 项和为
项和为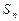 ,若
,若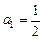 且
且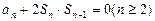 .
.(Ⅰ)求证
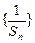 是等差数列,并求出
是等差数列,并求出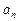 的表达式;
的表达式;(Ⅱ)若
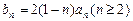 ,求证
,求证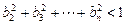 .
.(Ⅰ)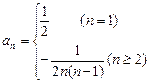 (Ⅱ)略
(Ⅱ)略
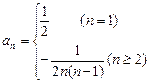 (Ⅱ)略
(Ⅱ)略(I)证明:∵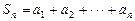
∴当n≥2时,an = Sn – Sn – 1--1分又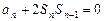
∴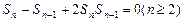 ,---3分
,---3分
若Sn = 0,则an = 0,∴a1 = 0与a1 =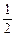 矛盾!∴Sn≠0,Sn – 1≠0.
矛盾!∴Sn≠0,Sn – 1≠0.
∴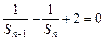 即
即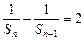 --5分又
--5分又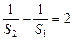 .
.
∴{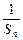 }是首项为2,公差为2的等差数列 ---6分
}是首项为2,公差为2的等差数列 ---6分
{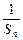 }是等差数列.∴
}是等差数列.∴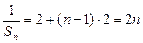 即
即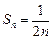 ---7分
---7分
∴当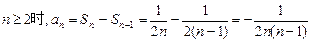 ----8分
----8分
又当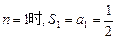 ∴
∴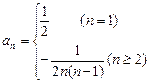 ---9分
---9分
(Ⅱ)证明:由(I)知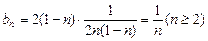 ----10分
----10分
∴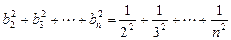
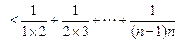 ---12分
---12分
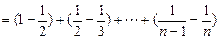
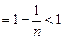 ------14分
------14分
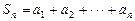
∴当n≥2时,an = Sn – Sn – 1--1分又
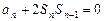
∴
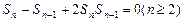 ,---3分
,---3分若Sn = 0,则an = 0,∴a1 = 0与a1 =
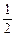 矛盾!∴Sn≠0,Sn – 1≠0.
矛盾!∴Sn≠0,Sn – 1≠0.∴
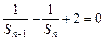 即
即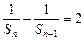 --5分又
--5分又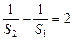 .
.∴{
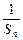 }是首项为2,公差为2的等差数列 ---6分
}是首项为2,公差为2的等差数列 ---6分{
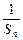 }是等差数列.∴
}是等差数列.∴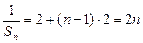 即
即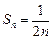 ---7分
---7分∴当
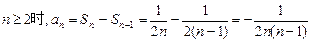 ----8分
----8分又当
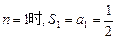 ∴
∴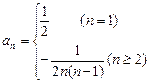 ---9分
---9分(Ⅱ)证明:由(I)知
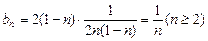 ----10分
----10分∴
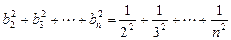
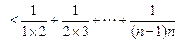 ---12分
---12分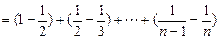
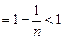 ------14分
------14分
练习册系列答案
相关题目
 列
列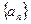 的前
的前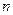 项和为
项和为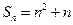 .
.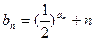 ,求数列
,求数列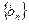 的前
的前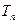 .
.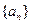 满足
满足 ,其中
,其中 ,函数
,函数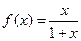 .
. ,
, ,求
,求 ; (2)若数列
; (2)若数列 .数列
.数列 满足
满足 ,求证:
,求证: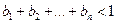 .
. , 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )
, 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )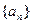 的前
的前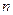 项和满足
项和满足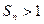 ,且
,且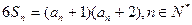 .(1)求
.(1)求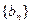 满足
满足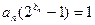 ,并记
,并记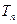 为
为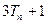 与
与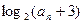 的大小.
的大小.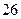 ,第二数与第三数之积为
,第二数与第三数之积为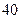 ,求这四个数
,求这四个数
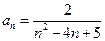 则{an}的最大项是
则{an}的最大项是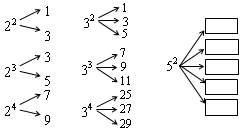
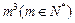 的“分裂”
的“分裂”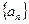 中,
中,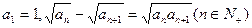 ,则
,则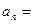 .
.