题目内容
已知f(x)=bx+1为x的一次函数, b为不等于1的常数, 且
g(n)= , 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )
, 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )
A 等差数列 B等比数列 C 递增数列 D 递减数列
g(n)=
 , 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )
, 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )A 等差数列 B等比数列 C 递增数列 D 递减数列
B
已知f(x)=bx+1为x的一次函数, b为不等于1的常数, 且
g(n)= ,
,
则g(1)=b+1,g(2)=b2+b+1,g(3)=b3+ b2+b+1, ┉,g(n)= +┉+ b2+b+1.
+┉+ b2+b+1.
a1=b,a2= b2,a3= b3,┉,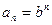
故数列{an} 是等比数列
g(n)=
 ,
, 则g(1)=b+1,g(2)=b2+b+1,g(3)=b3+ b2+b+1, ┉,g(n)=
 +┉+ b2+b+1.
+┉+ b2+b+1.a1=b,a2= b2,a3= b3,┉,
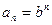
故数列{an} 是等比数列

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
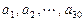 ,其中
,其中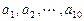 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;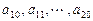 是公差为
是公差为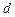 的等差数列;
的等差数列;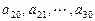 是公差为
是公差为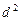 的等差数列(
的等差数列(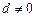 ).
).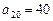 ,求
,求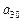 关于
关于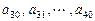 是公差为
是公差为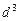 的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列.提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?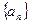 的前
的前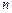 项和为
项和为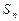 ,若
,若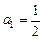 且
且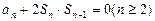 .
.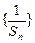 是等差数列,并求出
是等差数列,并求出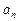 的表达式;
的表达式;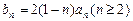 ,求证
,求证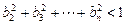 .
.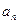 }中,
}中,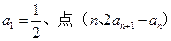 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….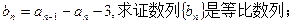 (Ⅱ)求数列
(Ⅱ)求数列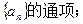
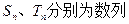
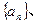
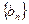 的前n项和,是否存在实数
的前n项和,是否存在实数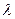 ,使得数列
,使得数列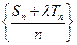 为等差数列?若存在,试求出
为等差数列?若存在,试求出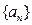 中,
中,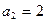 ,前
,前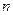 项和为
项和为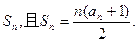
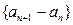 是等差数列,并求出数列
是等差数列,并求出数列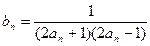 ,数列
,数列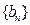 的前
的前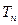 ,求使不等式
,求使不等式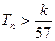 对一切
对一切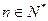 都成立的最大正整数
都成立的最大正整数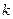 的值。
的值。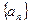 中,
中,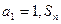 是数列
是数列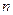 项和,对任意
项和,对任意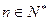 ,均有
,均有 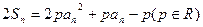 (1).求常数
(1).求常数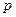 的值;(2)求数列
的值;(2)求数列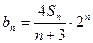 ,求数列
,求数列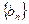 的前
的前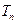 。
。  的前
的前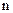 项和为
项和为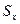 若
若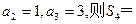
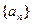 中,
中,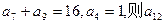 的值是( )
的值是( )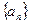 的首项
的首项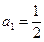 ,前n项和
,前n项和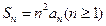
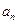 ;(2)记
;(2)记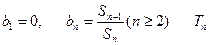 为数例
为数例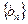 的前
的前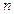 项和,求证
项和,求证