题目内容
【题目】对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x﹣[x],下列命题中正确命题的序号 .
①函数f(x)的最大值为1;
②函数f(x)的最小值为0;
③方程f(x)﹣ ![]() =0有无数个解;
=0有无数个解;
④函数f(x)是增函数;
⑤对任意的x∈R,函数f(x)满足f(x+1)=f(x);
⑥函数f(x)的图象与函数g(x)=|lgx|的图象的交点个数为10个.
【答案】②③⑤
【解析】解:定义函数f(x)=x﹣[x],其图象:x为整数时f(x)=0,x不为整数时f(x)∈(0,1)
可得:①函数f(x)的最大值为1,不正确;
②函数f(x)的最小值为0,正确;
③函数G(x)=f(x)﹣ ![]() 有无数个零点,正确;
有无数个零点,正确;
④函数f(x)是周期函数,不是增函数,因此不正确.
⑤函数f(x)是周期为1的函数,正确.
⑥函数f(x)的图象与函数g(x)=|lgx|的图象的交点个数为11个,不正确.
所以答案是:②③⑤.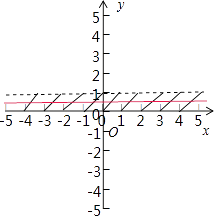
【考点精析】关于本题考查的命题的真假判断与应用,需要了解两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】2016年10月,继微信支付对提现转账收费后,支付宝也开始对提现转账收费,随着这两大目前用户使用粘度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取200人,把这200人分为3类:认为使用支付宝方便,仍使用支付宝提现转账的用户称为“![]() 类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“
类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“![]() 类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“
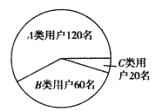
类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“![]() 类用户”,各类用户的人数如图所示:
类用户”,各类用户的人数如图所示:
同时把这200人按年龄分为青年人组与中老年人组,制成如图所示的![]() 列联表:
列联表:
| 非 | 合计 | |
青年 | 20 | ||
中老年 | 40 | ||
合计 | 200 |
(Ⅰ)完成![]() 列联表并判断是否有99.5%的把握认为“
列联表并判断是否有99.5%的把握认为“![]() 类用户与年龄有关”;
类用户与年龄有关”;
(Ⅱ)从这200人中按![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中
类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户均存在的概率;
类用户均存在的概率;
(Ⅲ)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用![]() 表示所选3人中
表示所选3人中![]() 类用户的人数,求
类用户的人数,求![]() 的分布列与期望.
的分布列与期望.
附:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)