题目内容
【题目】在平面直角坐标系
中,抛物线
,斜率为
的直线
经过
焦点,且与交于
两点满足
.
(1)求抛物线的方程；
(2)已知线段
的垂直平分线与抛物线交于
两点, 
为线段
的中点,记点到直线的距离为
,若
，求
的值.
【答案】(1)
;(2)
.
【解析】分析：(1)设
的方程：
，与抛物线方程联立，利用根与系数的关系表示
，即可得到结果； (2)由（1）可知
，
，设
的中点
，则
的中垂线
的方程：
，的方程与联立，利用根与系数关系表示R点坐标，从而得到
点到：
的距离，利用弦长公式表示
，由
，解得k的值.
详解：（1）由已知，的方程：，设
，
由
，得：
，
，
，
由已知得：
，
抛物线方程；
（2）由第（1）题知，
，
方程即：
，
，
设的中点，
则：
，
，
所以的中垂线的方程：
，即
将的方程与联立得：
，
设
，则
点到：的距离
所以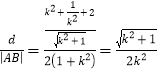
由已知得：
，得.
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
