Question

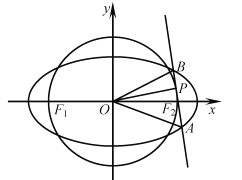
【题目】如图，在平面直角坐标系中，椭圆C过点，焦点，圆O的直径为．

（1）求椭圆C及圆O的方程；

（2）设直线l与圆O相切于第一象限内的点P．

①若直线l与椭圆C有且只有一个公共点，求点P的坐标；

②直线l与椭圆C交于两点．若的面积为，求直线l的方程．

Answer 1

【答案】（1）椭圆C的方程为；圆O的方程为

（2）①点P的坐标为；②直线l的方程为

【解析】分析：（1）根据条件易得圆的半径，即得圆的标准方程，再根据点在椭圆上，解方程组可得a,b，即得椭圆方程；（2）第一问先根据直线与圆相切得一方程，再根据直线与椭圆相切得另一方程，解方程组可得切点坐标.第二问先根据三角形面积得三角形底边边长，再结合①中方程组，利用求根公式以及两点间距离公式，列方程，解得切点坐标，即得直线方程.

详解：解：（1）因为椭圆C的焦点为，

可设椭圆C的方程为．又点在椭圆C上，

所以，解得

因此，椭圆C的方程为．

因为圆O的直径为，所以其方程为．

（2）①设直线l与圆O相切于，则，

所以直线l的方程为，即．

由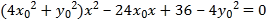，消去y，得

．（*）

因为直线l与椭圆C有且只有一个公共点，

所以．

因为，所以．

因此，点P的坐标为．

②因为三角形OAB的面积为，所以，从而．

设，

由（*）得，

所以

．

因为，

所以，即，

解得舍去），则，因此P的坐标为．

综上，直线l的方程为．