题目内容
设数列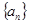 为等差数列,且
为等差数列,且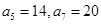 ,数列
,数列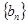 的前
的前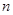 项和为
项和为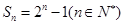 ,
,
(1)求数列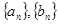 的通项公式;
的通项公式;
(2)若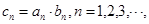 ,求数列
,求数列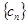 的前
的前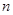 项和
项和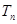 .
.
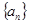 为等差数列,且
为等差数列,且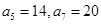 ,数列
,数列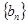 的前
的前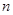 项和为
项和为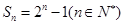 ,
,(1)求数列
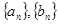 的通项公式;
的通项公式;(2)若
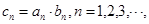 ,求数列
,求数列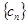 的前
的前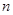 项和
项和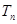 .
. (1) ,
,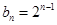 ;(2)
;(2)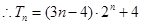
 ,
,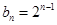 ;(2)
;(2)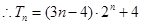
试题分析: (1)由等差数列的通项公式
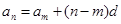 求公差
求公差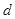 ,即可求
,即可求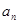 ;利用
;利用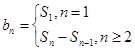 ,求
,求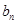 ;(2)
;(2)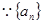 是等差数列,
是等差数列,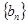 是等比数列,
是等比数列,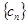 是由两者相乘,
是由两者相乘,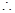 利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量(
利用错位相减法求和即可.规律总结:1.等差数列的求解问题,要抓住五个基本量( ),一般题型是“知三求二”,利用方程思想(关于
),一般题型是“知三求二”,利用方程思想(关于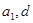 的方程)进行求有关量;2对于
的方程)进行求有关量;2对于 (其中
(其中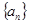 是等差数列,
是等差数列,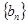 是等比数列)的求和问题,要利用错位相减法(乘公比
是等比数列)的求和问题,要利用错位相减法(乘公比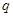 后,错位相减).
后,错位相减).注意点:错位相减法,一定要向后错一位,使同次数的项对齐,以便正确化简;一定要搞清相减后,有多少项可构成等比数列.
试题解析:
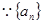 是等差数列,
是等差数列,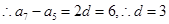
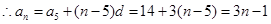
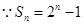 ,
,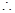 当
当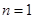 时,
时,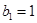 ;当
;当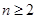 时,
时,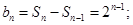
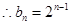 .
.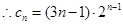
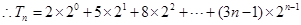
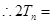
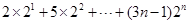
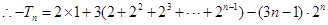

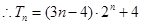
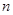 项和.
项和.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 满足:
满足: ,
, 的前
的前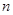 项和为
项和为 .
. 及
及 (其中
(其中 为常数,且
为常数,且 ),求证数列
),求证数列 为等比数列.
为等比数列. 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
 ,数列
,数列 的前
的前 ,求满足
,求满足 的
的 满足
满足 ,
,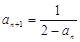
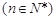 .
.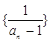 为等差数列,并求出
为等差数列,并求出 ,数列
,数列 的前
的前 项和为
项和为 ,对任意
,对任意 都有
都有 成立,求整数
成立,求整数 的最大值.
的最大值.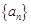 为等差数列,首项
为等差数列,首项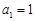 ,公差
,公差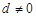 ,若
,若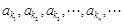 成等比数列,且
成等比数列,且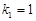 ,
,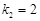 ,
,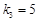 ,则
,则 .
.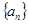 为等差数列,若
为等差数列,若 ,且它们的前n项和
,且它们的前n项和 有最大值,
有最大值, 的n的最大值为( ).
的n的最大值为( ).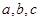 成等差数列,
成等差数列,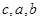 成等比数列,且
成等比数列,且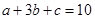 ,则
,则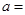
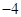
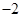
 满足
满足 ,
,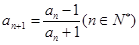 ,则
,则 ( )
( )

