题目内容
数列 满足
满足 ,
,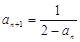
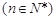 .
.
(1)求证: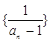 为等差数列,并求出
为等差数列,并求出 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,对任意
,对任意 都有
都有 成立,求整数
成立,求整数 的最大值.
的最大值.
 满足
满足 ,
,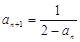
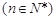 .
.(1)求证:
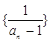 为等差数列,并求出
为等差数列,并求出 的通项公式;
的通项公式;(2)设
 ,数列
,数列 的前
的前 项和为
项和为 ,对任意
,对任意 都有
都有 成立,求整数
成立,求整数 的最大值.
的最大值.(1) (2)18
(2)18
 (2)18
(2)18试题分析:(1)要证明
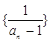 是等差数列,只需证明
是等差数列,只需证明 是常数,所以根据题意,利用
是常数,所以根据题意,利用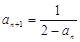 ,化简
,化简 ,即可证明.
,即可证明.(2)将(1)中结论代入
 ,而后设出
,而后设出 ,根据题意只需找到
,根据题意只需找到 的最小值,令最小值大于
的最小值,令最小值大于 .所以得判断数列
.所以得判断数列 的增减性,利用
的增减性,利用 ,放缩判断其与0的大小关系.而后根据
,放缩判断其与0的大小关系.而后根据 ,可得结论.
,可得结论.试题解析:(1)




∴

∴
 为首次为-2,公差为-1的等差数列
为首次为-2,公差为-1的等差数列∴


∴

(2)
 令
令
∴
 =
=
=

∴
 ∴
∴ 为单调递增数列
为单调递增数列∴
 ∴
∴
∴
 又
又 所以
所以 的最大值为18
的最大值为18
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
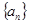 为等差数列,且
为等差数列,且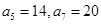 ,数列
,数列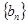 的前
的前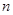 项和为
项和为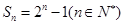 ,
,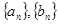 的通项公式;
的通项公式;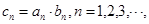 ,求数列
,求数列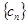 的前
的前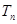 .
.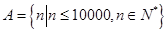 中所有的完全平方数和完全立方数后,将剩下的元素按从
中所有的完全平方数和完全立方数后,将剩下的元素按从 中,若
中,若 ,
, ,则
,则 .
.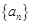 中,若对任意的
中,若对任意的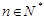 均有
均有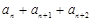 为定值,且
为定值,且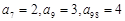 ,则数列
,则数列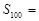 ( )
( ) =( )
=( )

 ,且
,且 ,则
,则 的值为( )
的值为( )

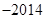
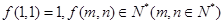 ,且对任意
,且对任意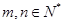 都有
都有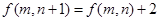 ;②
;②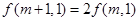 。则
。则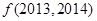 的值为____________。
的值为____________。