题目内容
已知数列{an}:a1,a2,a3,…,an,如果数列{bn}:b1,b2,b3,…,bn满足b1=an,bk=ak-1+ak-bk-1,其中k=2,3,…,n,则称{bn}为{an}的“衍生数列”.若数列{an}:a1,a2,a3,a4的“衍生数列”是5,-2,7,2,则{an}为________;若n为偶数,且{an}的“衍生数列”是{bn},则{bn}的“衍生数列”是________.
2,1,4,5 {an}
由b1=an,bk=ak-1+ak-bk-1,k=2,3,…,n可得,a4=5,2=a3+a4-7,解得a3=4.又7=a2+a3-(-2),解得a2=1.由-2=a1+a2-5,解得a1=2,所以数列{an}为2,1,4,5.
由已知,b1=a1-(a1-an),b2=a1+a2-b1=a2+(a1-an),….
因为n是偶数,所以bn=an+(-1)n(a1-an)=a1.设{bn}的“衍生数列”为{cn},则ci=bi+(-1)i(b1-bn)=ai+(-1)i·(a1-an)+(-1)i(b1-bn)=ai+(-1)i(a1-an)+(-1)i·(an-a1)=ai,其中i=1,2,3,…,n.则{bn}的“衍生数列”是{an}.
由已知,b1=a1-(a1-an),b2=a1+a2-b1=a2+(a1-an),….
因为n是偶数,所以bn=an+(-1)n(a1-an)=a1.设{bn}的“衍生数列”为{cn},则ci=bi+(-1)i(b1-bn)=ai+(-1)i·(a1-an)+(-1)i(b1-bn)=ai+(-1)i(a1-an)+(-1)i·(an-a1)=ai,其中i=1,2,3,…,n.则{bn}的“衍生数列”是{an}.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
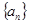 为等差数列,且
为等差数列,且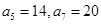 ,数列
,数列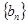 的前
的前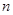 项和为
项和为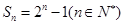 ,
,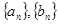 的通项公式;
的通项公式;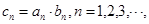 ,求数列
,求数列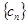 的前
的前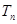 .
.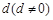 的等差数列,已知它的前10项和为
的等差数列,已知它的前10项和为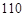 ,且a1,a2,a4 成等比数列.
,且a1,a2,a4 成等比数列.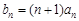 ,求数列
,求数列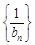 的前
的前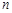 项和Tn .
项和Tn . =( )
=( )

 (i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如
(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如 =8,则
=8,则 为 。
为 。
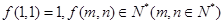 ,且对任意
,且对任意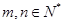 都有
都有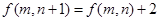 ;②
;②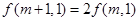 。则
。则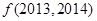 的值为____________。
的值为____________。