题目内容
【题目】在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() :ρ(2cosθ-sinθ)=6.
:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的![]() 、2倍后得到曲线C2,试写出直线
、2倍后得到曲线C2,试写出直线![]() 的直角坐标方程和曲线C2的参数方程.
的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
【答案】(Ⅰ)![]() ,
,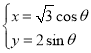 ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】
(Ⅰ)根据极坐标与普通方程的互化公式,将直线![]() :ρ(2cosθ-sinθ)=6化为参数方程,C2的方程为
:ρ(2cosθ-sinθ)=6化为参数方程,C2的方程为![]() ,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.
,化为普通方程;(Ⅱ)利用点到直线的距离公式表示出距离,求最值.
(Ⅰ)由题意知,直线![]() 的直角坐标方程为:2x-y-6=0.
的直角坐标方程为:2x-y-6=0.
∵C2:(![]() =1 ∴C2:的参数方程为:
=1 ∴C2:的参数方程为: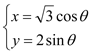 (θ为参数);
(θ为参数);
(Ⅱ)设P(![]() cosθ,2sinθ),则点P到
cosθ,2sinθ),则点P到![]() 的距离为
的距离为
d=![]() ,
,
∴当sin(60°-θ)=-1,即点P(-![]() ,1)时,此时
,1)时,此时![]()
![]() =2
=2![]() .
.

练习册系列答案
相关题目
【题目】某高三理科班共有![]() 名同学参加某次考试,从中随机挑出
名同学参加某次考试,从中随机挑出![]() 名同学,他们的数学成绩
名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 |
|
|
|
|
|
物理成绩 |
|
|
|
|
|
(1)数据表明![]() 与
与![]() 之间有较强的线性关系,求
之间有较强的线性关系,求![]() 于
于![]() 的线性回归方程;
的线性回归方程;
(2)本次考试中,规定数学成绩达到![]() 分为优秀,物理成绩达到
分为优秀,物理成绩达到![]() 分为优秀.若该班数学优秀率与物理优秀率分别为
分为优秀.若该班数学优秀率与物理优秀率分别为![]() 和
和![]() ,且除去抽走的
,且除去抽走的![]() 名同学外,剩下的同学中数学优秀但物理不优秀的同学共有
名同学外,剩下的同学中数学优秀但物理不优秀的同学共有![]() 人,请写出
人,请写出![]() 列联表,判断能否在犯错误的概率不超过
列联表,判断能否在犯错误的概率不超过![]() 的前提下认为数学优秀与物理优秀有关?
的前提下认为数学优秀与物理优秀有关?
参考数据: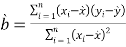 ,
,![]() ;
;![]() ,
,![]() ;
;![]()