题目内容
【题目】设函数
，
.
（1）当
（
为自然对数的底数）时，求
的极小值；
（2）讨论函数
零点的个数.
【答案】（1）极小值
；
（2）①当
时，
无零点，
②当
或
时，有且仅有
个零点，
③当
时，有两个零点.
【解析】
试题（1）要求
的极小值，可以通过判断其单调性从而求得其极小值，对求导，可知
，再通过列表即可得当
时，
取得极小值
；（2）令
，可得
，因此要判断函数
的零点个数，可通过画出函数
的草图来判断，同样可以通过求导判断函数的单调性来画出函数图象的草图：
，通过列表可得到
的单调性，作出
的图象，进而可得
①当
时，
无零点，②当或
时，有且仅有个零点，
③当
时，有两个零点.
试题解析：（1）当
时，
，其定义域为
，
，
令
，，
|
|
|
|
|
|
|
|
|
| 极小值 |
|
故当时，取得极小值；
（2）
，其定义域为，
令
，得，
设
，其定义域为.则的零点为与
的交点，
，
|
|
|
|
|
|
|
|
|
| 极大值 |
|
故当
时，取得最大值
作出的图象，可得
①当时，无零点，
②当或时，有且仅有个零点，
③当时，有两个零点.
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值
与销售单价
之间的关系,经统计得到如下数据：
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；
（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？
参考公式：对一组数据
,
，····
,其回归直线
的斜率和截距最小二乘估计分别为：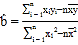
,
.
参考数据：
,
.
【题目】某小型企业甲产品生产的投入成本x（单位：万元）与产品销售收入y（单位：万元）存在较好的线性关系，下表记录了最近5次该产品的相关数据.
x（万元） | 3 | 5 | 7 | 9 | 11 |
y（万元） | 8 | 10 | 13 | 17 | 22 |
（1）求y关于x的线性回归方程；
（2）根据（1）中的回归方程，判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大（毛利率
）？
相关公式：
，
.
