题目内容
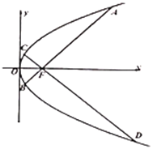
【题目】已知抛物线
，过抛物线C的焦点F作互相垂直的两条直线AB，CD，与抛物线C分别相交于A，B和C，D，点A，C在x轴上方.
（1）若直线AB的倾斜角为
，求
的值；
（2）设
与
的面积之和为S，求S的最小值.
【答案】（1）
（2）8
【解析】
（1）先求出直线直线AB的方程为
，与抛物线方程联立，根据韦达定理和抛物线的性质即可求出；
（2）设直线AB的方程为
，则CD为
，分别根据韦达定理和基本不等式即可求出S的最小值.
解：（1）直线AB的方程为，设
，
，
由
，消y可得
，
∴
，
∴
.
（2）由已知条件得直线AB的斜率存在且不为0，设直线AB的方程为，则CD为，
设，，
，
，
由
，消y可得
，
∴
，
，
∴
，
∴
，
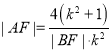由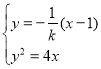
，消y可得
，
∴
1，，
∴
，
∴
∴
，
当且仅当
时等号成立，
故S的最小值为8.
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
