Question

【题目】已知⊙C过点P（1，1），且与⊙M：（x+2）2+（y+2）2=r2（r＞0）关于直线x+y+2=0对称．
（1）求⊙C的方程；
（2）设Q为⊙C上的一个动点，求 的最小值．

Answer 1

【答案】
（1）解：设圆心C（a，b），则 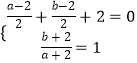，解得 a=0，b=0

则圆C的方程为x2+y2=r2，

将点P的坐标（1，1）代入得r2=2，

故圆C的方程为x2+y2=2；

（2）解：设Q（x，y），则x2+y2=2，

=（x﹣1，y﹣1）（x+2，y+2）=x2+y2+x+y﹣4=x+y﹣2，

令x= cosθ，y= sinθ，

∴ = cosθ+ sinθ﹣2=2sin（θ+ ）﹣2，

∴θ+ =2kπ﹣ 时，sin（θ+ ）的最小值为﹣1，

所以 的最小值为﹣2﹣2=﹣4

【解析】（1）设圆心的坐标，利用对称的特征，建立方程组，从而求出圆心坐标，又⊙C过点P（1，1），可得半径，故可写出⊙C方程．（2）设Q的坐标，用坐标表示两个向量的数量积，化简后再进行三角代换，可得其最小值．