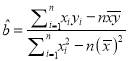Question

【题目】已知函数f（x）= （a＞0）
（1）若a=1，证明：y=f（x）在R上单调递减；
（2）当a＞1时，讨论f（x）零点的个数．

Answer 1

【答案】
（1）当a=1时，且x≥1时，f（x）=lnx﹣x+1，

∴0恒成立，

∴f（x）在[1，+∞）单调递减，

当x＜1时，f（x）=ex﹣1﹣x，

∴f′（x）=ex﹣1﹣1＜0恒成立，

∴f（x）在（﹣∞，1）单调递减，

综上所述y=f（x）在R上单调递减

（2）解：当x≥a时，f（x）=lnx﹣ax+1=0，分别画出y=lnx，与y=ax﹣1的图象，如图所示：

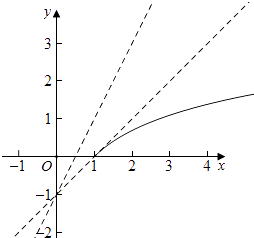
∵y=ax﹣1过定点（0，﹣1），

设直线y=ax﹣1与y=lnx的切点为（m，n），

∴k=f′（m）= = ，f（m）=lnm=n

∴n=0，m=1，

由图象可知，x≥a时，且当a＞1时，图象无交点，故f（x）无零点，

当x＜a时，f（x）=ex﹣1+（a﹣2）x，

分别画出y=ex﹣1，与y=（2﹣a）x的图象，如图所示：

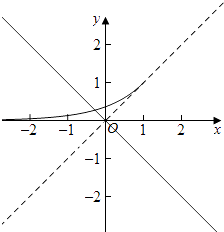
∵y=（2﹣a）x过定点（0，0），

由图象可知，当a＞2时，图象有一个交点，故f（x）有一个零点，

当1＜a≤2时，图象无交点，故f（x）无零点，

故x＜a时，函数f（x）有一个零点，

综上所述，当a＞2时，故f（x）有一个零点，当1＜a≤2时，故f（x）无零点．

【解析】（1）分类讨论，根据导数和函数的单调性的关系即可证明；（2）利用数形结合法，分段讨论，即可求出函数的零点的个数．
【考点精析】根据题目的已知条件，利用函数单调性的判断方法的相关知识可以得到问题的答案，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较．